Parçalı Fonksiyonların Türevi
Konu tekrarı için: Parçalı Fonksiyonlar | Parçalı Fonksiyonların Limiti | Parçalı Fonksiyonların Sürekliliği
Tanım kümesinin farklı aralıklarında farklı tanımlara sahip olan fonksiyonlara parçalı fonksiyon denir. Bir parçalı fonksiyonun farklı tanıma sahip olduğu alt aralıklara fonksiyonun dalları ya da parçaları, fonksiyon tanımının değiştiği noktalara fonksiyonun geçiş noktaları denir.
Bir parçalı fonksiyonun bir geçiş noktasında türevlenebilir olması için, türevlenebilirlik tanımı gereği bu noktanın her iki tarafında tanımlı olan fonksiyonların bu noktadaki soldan ve sağdan türevleri tanımlı ve birbirine eşit olmalıdır.
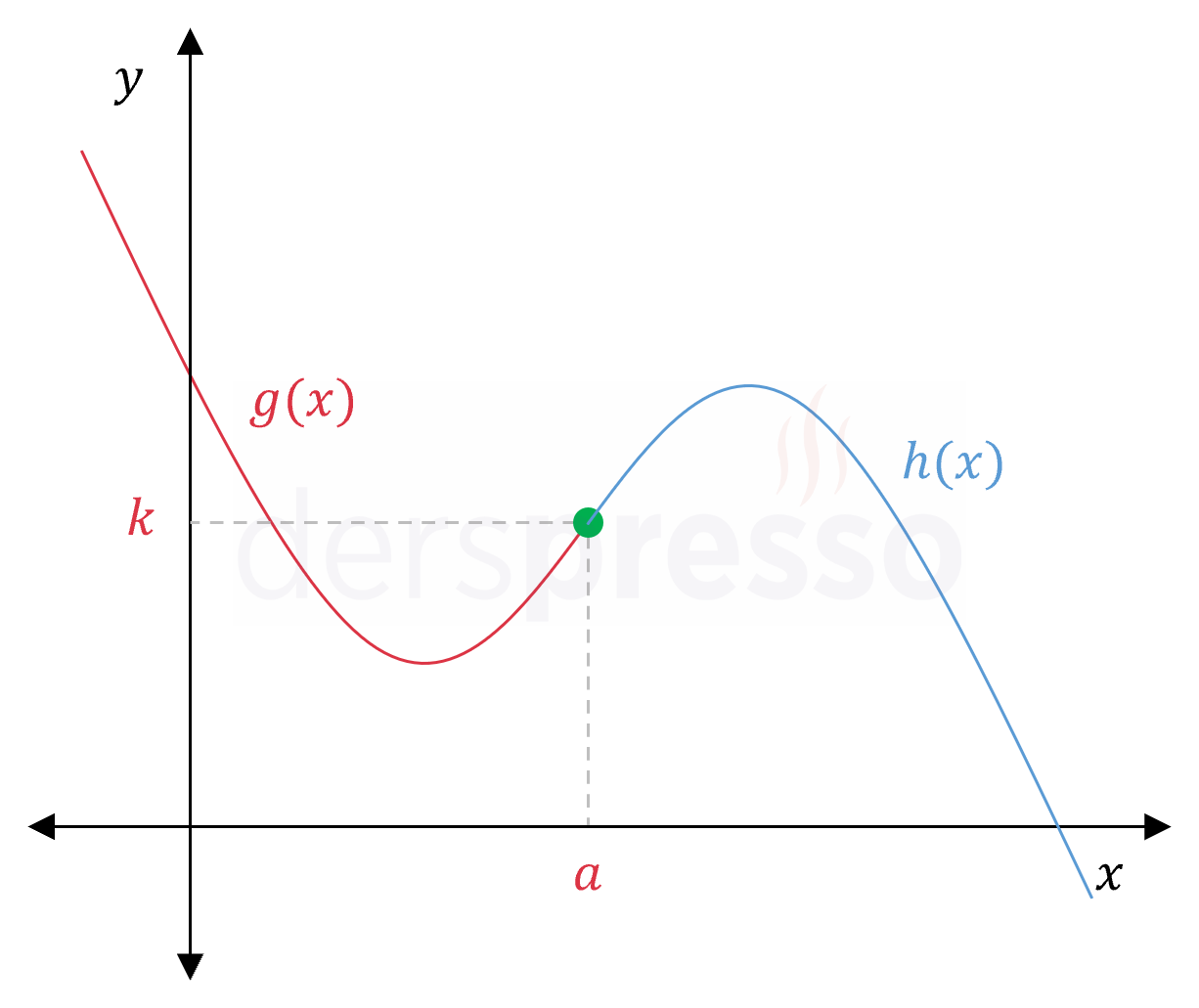
\( a, k \in \mathbb{R} \) olmak üzere,
\( f(x) = \begin{cases} g(x) & x \lt a \\ k & x = a \\ h(x) & x \gt a \end{cases} \)
parçalı fonksiyonunun \( x = a \) noktasında soldan ve sağdan türevleri birer reel sayı olarak tanımlı ve birbirine eşit ise fonksiyon bu noktada türevlenebilirdir.
\( g'(a^-) = h'(a^+) = f'(a) \)
Aksi takdirde fonksiyon bu noktada türevlenebilir değildir.
Bir parçalı fonksiyonun bir geçiş noktasında türevlenebilirlik iki şekilde kontrol edilebilir.
- Türevin limit tanımı ile: Türevin limit tanımı bir noktadaki sürekliliği de kapsadığı için ilgili noktada ek olarak süreklilik kontrolüne gerek yoktur.
- Türev alma kuralları ile: Bu durumda türevlenebilirlik öncesinde ilgili noktada süreklilik kontrolü yapılmalıdır.
Parçalı fonksiyonların geçiş noktalarındaki türevlenebilirliğini her iki yöntemi de kullanarak birkaç örnek üzerinden inceleyelim.
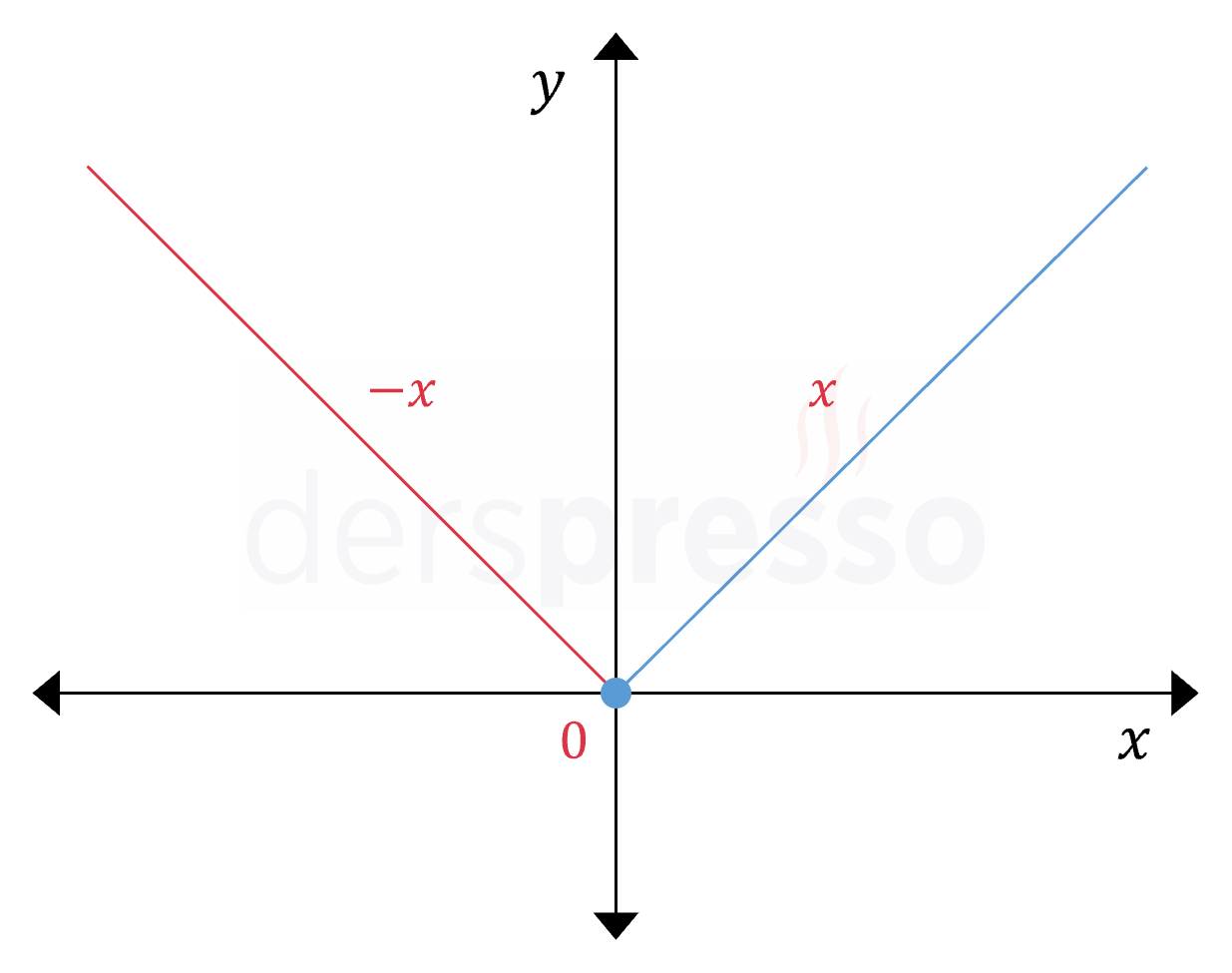
\( f(x) = \begin{cases} -x & x \lt 0 \\ x & x \ge 0 \end{cases} \)
parçalı fonksiyonunun \( x = 0 \) noktasında türevlenebilir olup olmadığını bulalım.
\( x = 0 \) parçalı fonksiyonun geçiş noktasıdır.
Bir parçalı fonksiyonun bir geçiş noktasında türevlenebilir olması için, bu noktanın her iki tarafında tanımlı olan fonksiyonların bu noktadaki soldan ve sağdan türevleri tanımlı ve birbirine eşit olmalıdır.
Fonksiyonun \( x = 0 \) noktasındaki soldan ve sağdan türevlenebilirliğini türevin limit tanımını kullanarak bulalım.
Fonksiyonun \( x = 0 \) noktasındaki soldan türevi:
\( f'(a^-) = \lim\limits_{x \to a^-} {\dfrac{f(x) - f(a)}{x - a}} \)
\( f'(0^-) = \lim\limits_{x \to 0^-} {\dfrac{-x - 0}{x - 0}} = -1 \)
Fonksiyonun \( x = 0 \) noktasındaki sağdan türevi:
\( f'(a^+) = \lim\limits_{x \to a^+} {\dfrac{f(x) - f(a)}{x - a}} \)
\( f'(0^+) = \lim\limits_{x \to 0^+} {\dfrac{x - 0}{x - 0}} = 1 \)
Buna göre bu noktada soldan ve sağdan türevler birer reel sayı olarak tanımlıdır, ancak birbirine eşit değildir, dolayısıyla fonksiyon \( x = 0 \) noktasında türevlenebilir değildir.
\( f'(0^-) \ne f'(0^+) \)
Aşağıdaki grafikte fonksiyonun bu noktada sürekli olduğu, ancak soldan ve sağdan türevlerinin farklı olduğu görülebilir.
\( f(x) = \begin{cases} -2 & x \lt 4 \\ 5 & x \ge 4 \end{cases} \)
parçalı fonksiyonunun \( x = 4 \) noktasında türevlenebilir olup olmadığını bulalım.
\( x = 4 \) parçalı fonksiyonun geçiş noktasıdır.
Fonksiyon tanımını incelediğimizde fonksiyonun bu noktada sürekli olmadığını görebiliriz. Bir fonksiyon sürekli olmadığı bir noktada türevlenebilir de değildir.
Fonksiyonun sürekli olmadığını gösterdikten sonra türevlenebilirlik için ek bir işlem yapmamıza gerek olmasa da, türevin limit tanımı ile soldan ve sağdan türevleri bularak fonksiyonun bu noktada türevlenebilir olmadığını gösterelim.
Fonksiyonun \( x = 4 \) noktasındaki soldan türevi:
\( f'(a^-) = \lim\limits_{x \to a^-} {\dfrac{f(x) - f(a)}{x - a}} \)
\( f'(4^-) = \lim\limits_{x \to 4^-} {\dfrac{-2 - 5}{x - 4}} = +\infty \)
Fonksiyonun \( x = 4 \) noktasındaki sağdan türevi:
\( f'(a^+) = \lim\limits_{x \to a^+} {\dfrac{f(x) - f(a)}{x - a}} \)
\( f'(4^+) = \lim\limits_{x \to 4^+} {\dfrac{5 - 5}{x - 4}} = 0 \)
Buna göre soldan türev bir reel sayı olarak tanımlı değildir, dolayısıyla fonksiyon \( x = 4 \) noktasında türevlenebilir değildir.
Aşağıdaki grafikte fonksiyonun bu noktada sürekli olmadığı görülebilir.

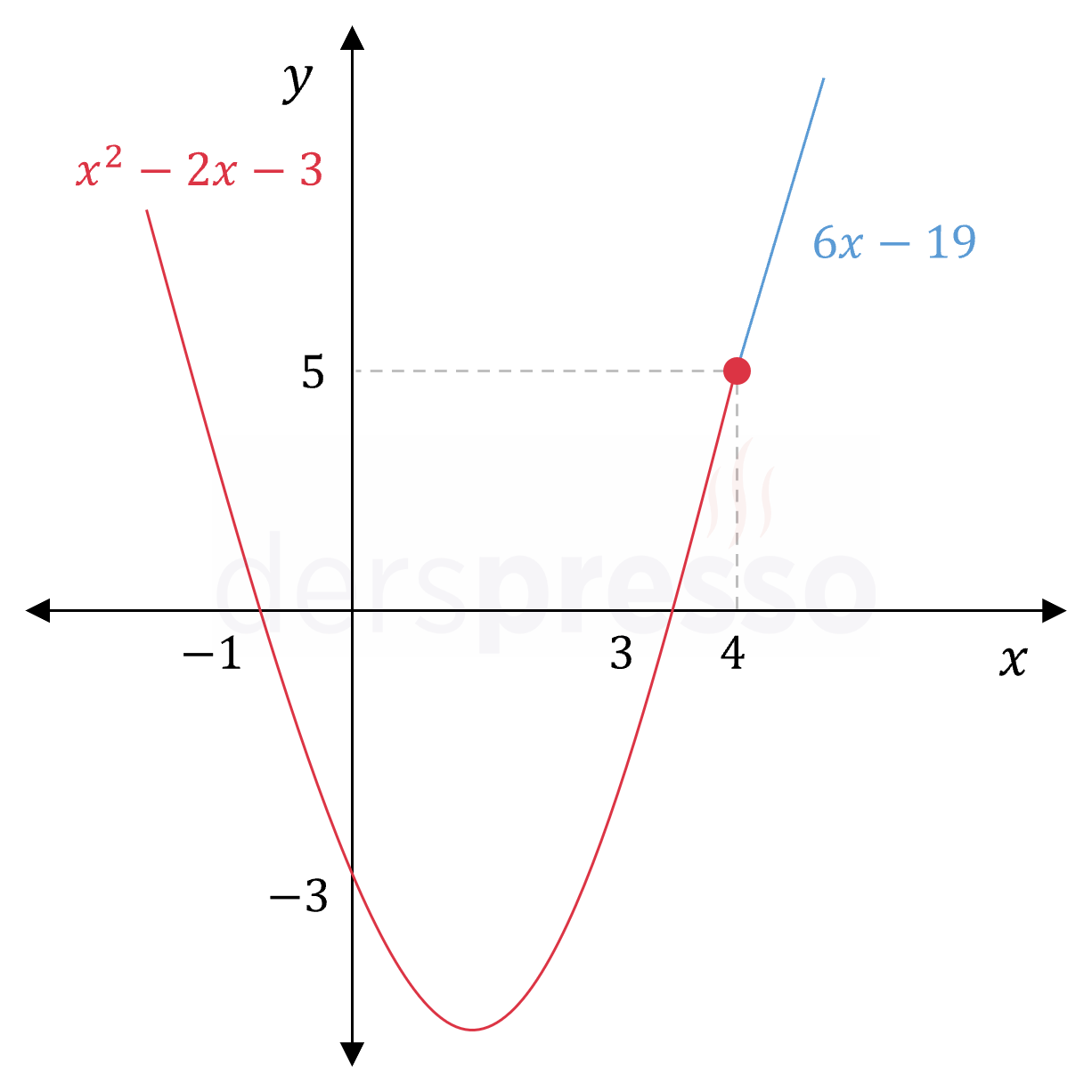
\( f(x) = \begin{cases} x^2 - 2x - 3 & x \le 4 \\ 6x - 19 & x \gt 4 \end{cases} \)
parçalı fonksiyonunun \( x = 4 \) noktasında türevlenebilir olup olmadığını bulalım.
Fonksiyonun \( x = 4 \) noktasındaki soldan ve sağdan türevlenebilirliğini türev alma kurallarını kullanarak bulalım.
Türev alma kurallarını kullanmadan önce bu noktadaki sürekliliği kontrol etmemiz gerekir.
Fonksiyonun \( x = 4 \) noktasındaki soldan limiti:
\( \lim\limits_{x \to 4^-} f(x) = \lim\limits_{x \to 4^-} (x^2 - 2x - 3) \)
\( = 4^2 - 2(4) - 3 = 5 \)
Fonksiyonun \( x = 4 \) noktasındaki sağdan limiti:
\( \lim\limits_{x \to 4^+} f(x) = \lim\limits_{x \to 4^+} (6x - 19) \)
\( = 6(4) - 19 = 5 \)
\( x = 4 \) noktasındaki fonksiyon değeri:
\( f(4) = 4^2 - 2(4) - 3 = 5 \)
Buna göre bu noktada soldan ve sağdan limitler ve fonksiyon değeri birer reel sayı olarak tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = 4 \) noktasında süreklidir.
\( f(4^-) = f(4^+) = f(4) \)
Sürekliliğini gösterdiğimiz bu noktadaki türevlenebilirliği kontrol edelim.
\( f'(x) = \begin{cases} 2x - 2 & x \le 4 \\ 6 & x \gt 4 \end{cases} \)
Fonksiyonun \( x = 4 \) noktasındaki soldan türevi:
\( f'(4^-) = 2(4) - 2 = 6 \)
Fonksiyonun \( x = 4 \) noktasındaki sağdan türevi:
\( f'(4^+) = 6 \)
Buna göre bu noktada soldan ve sağdan türevler tanımlıdır ve birbirine eşittir, dolayısıyla fonksiyon \( x = 4 \) noktasında türevlenebilirdir.
\( f'(4^-) = f'(4^+) = 6 \)
Aşağıdaki grafikte fonksiyonun bu noktada sürekli ve soldan/sağdan türevlerinin eşit olduğu görülebilir.
Bir parçalı fonksiyonun geçiş noktası olmayan bir noktasında türevlenebilir olup olmadığını bulmak için, bu noktanın bulunduğu aralıkta tanımlı olan fonksiyon kullanılarak türevlenebilirlik kontrol edilir.
Aşağıda grafiği verilen fonksiyonun \( x \in \{-6, -2, 2, 6\} \) noktalarında türevlenebilirliğini inceleyin.
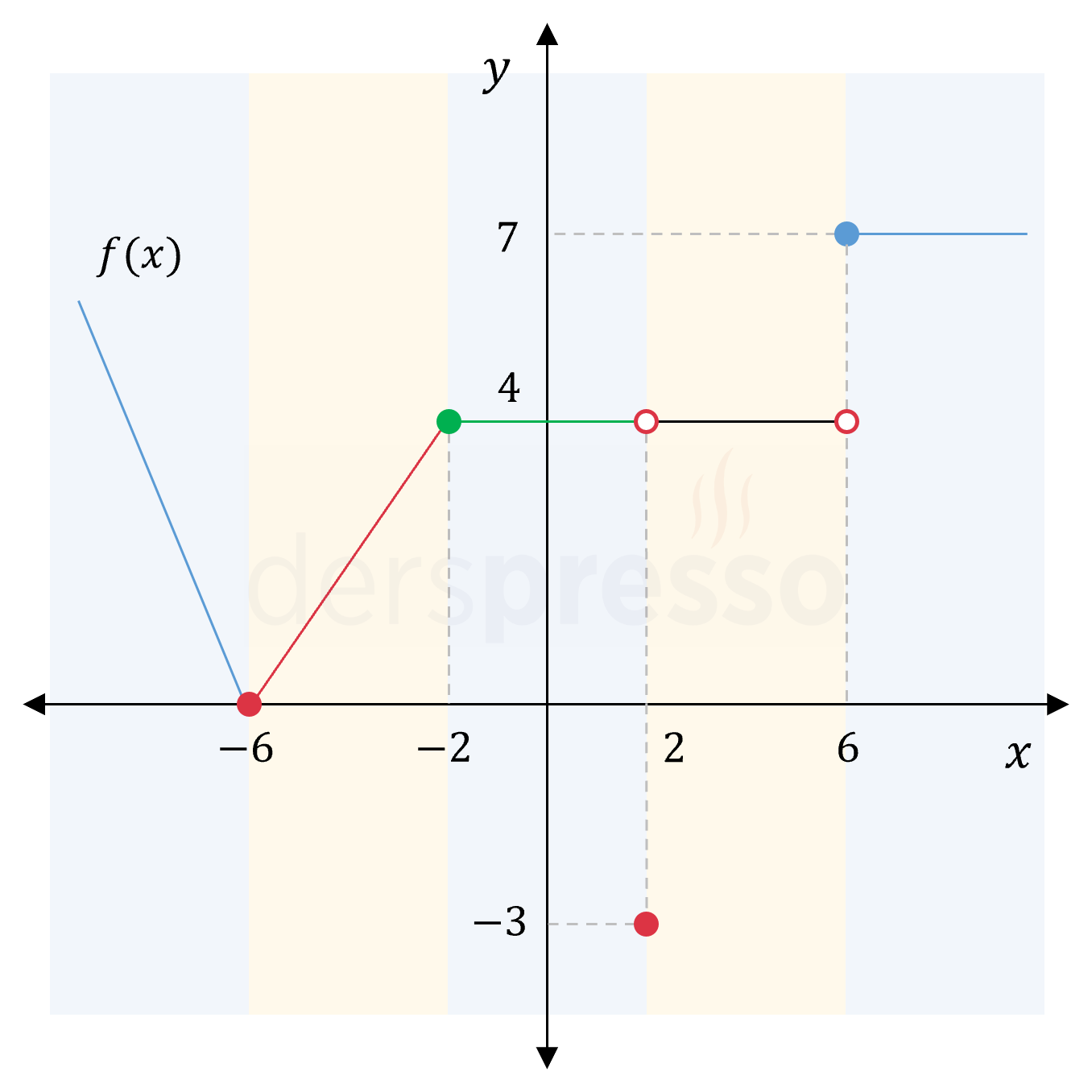
Bir fonksiyonun bir noktada türevlenebilir olması için bu noktadaki soldan ve sağdan türevler birer reel sayı olarak tanımlı ve birbirine eşit olmalıdır. Türevlenebilirlik tanımı sürekliliği de içerdiği için, bir noktada sürekli olmayan bir fonksiyon o noktada türevlenebilir de değildir.
Fonksiyon \( x = -6 \) noktasında süreklidir, ancak soldan ve sağdan türevler birbirine eşit değildir. Bu yüzden fonksiyon bu noktada türevlenebilir değildir.
Fonksiyon \( x = -2 \) noktasında süreklidir, ancak soldan ve sağdan türevler eşit değildir. Bu yüzden fonksiyon bu noktada türevlenebilir değildir.
Fonksiyonun \( x = 2 \) noktasında soldan ve sağdan limit değerleri eşit olsa da bu noktadaki fonksiyon değeri farklı olduğu için fonksiyon bu noktada süreksizdir. Bu yüzden fonksiyon bu noktada türevlenebilir değildir.
Fonksiyonun \( x = 6 \) noktasında soldan ve sağdan limit değerleri eşit olmadığı için fonksiyon bu noktada süreksizdir. Bu yüzden fonksiyon bu noktada türevlenebilir değildir.
\( f(x) = \begin{cases} x^2 + x & x \lt 1 \\ 2 & x = 1 \\ x^3 + 1 & x \gt 1 \end{cases} \)
fonksiyonunun \( x = 1 \) noktasındaki türevlenebilirliğini inceleyin.
Çözümü Göster\( x = 1 \) noktası parçalı fonksiyonun geçiş noktasıdır.
Fonksiyonun bu noktadaki soldan ve sağdan türevlenebilirliğini türev alma kurallarını kullanarak bulalım.
Türev alma kurallarını kullanmadan önce bu noktadaki sürekliliği kontrol etmemiz gerekir.
Parçalı fonksiyonunun her iki tanımındaki ifadeler birer polinom fonksiyonudur. Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
Fonksiyonun \( x = 1 \) noktasındaki soldan limiti:
\( \lim\limits_{x \to 1^-} f(x) = \lim\limits_{x \to 1^-} (x^2 + x) \)
\( = 1^2 + 1 = 2 \)
Fonksiyonun \( x = 1 \) noktasındaki sağdan limiti:
\( \lim\limits_{x \to 1^+} f(x) = \lim\limits_{x \to 1^+} (x^3 + 1) \)
\( = 1^3 + 1 = 2 \)
\( x = 1 \) noktasındaki fonksiyon değeri:
\( f(1) = 2 \)
Buna göre bu noktada soldan ve sağdan limitler ve fonksiyon değeri birer reel sayı olarak tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = 1 \) noktasında süreklidir.
\( f(1^-) = f(1^+) = f(1) \)
Sürekliliğini gösterdiğimiz bu noktadaki türevlenebilirliği kontrol edelim.
Fonksiyonun \( x = 1 \) noktasındaki soldan türevi:
\( f'(x) = 2x + 1 \)
\( f'(1^-) = 2(1) + 1 = 3 \)
Fonksiyonun \( x = 1 \) noktasındaki sağdan türevi:
\( f'(x) = 3x^2 \)
\( f'(1^+) = 3(1)^2 = 3 \)
Buna göre bu noktada soldan ve sağdan türevler tanımlıdır ve birbirine eşittir, dolayısıyla fonksiyon \( x = 1 \) noktasında türevlenebilirdir.
\( f'(1^-) = f'(1^+) = 3 \)
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = \abs{x^2 - 2x - 8} \) fonksiyonunun \( x = 2 \) noktasındaki türev değeri kaçtır?
Çözümü GösterFonksiyonu çarpanlarına ayıralım.
\( f(x) = \abs{(x + 2)(x - 4)} \)
Fonksiyonun kritik noktaları mutlak değer içini sıfır yapan \( x \in \{-2, 4\} \) noktalarıdır.
\( x = 2 \) bir kritik nokta olmadığı için fonksiyonun bu değerin bulunduğu aralıktaki fonksiyon tanımını kullanarak türev değerini bulalım.
\( (-2, 4) \) aralığında mutlak değer içindeki ifade negatif olur, dolayısıyla mutlak değerden negatif işaretli olarak çıkar.
\( (-2, 4) \) aralığı için:
\( f(x) = -(x^2 - 2x - 8) = -x^2 + 2x + 8 \)
Polinom fonksiyonları tüm reel sayılarda sürekli ve türevlenebilir olduğu için türev alma kuralları ile türevi alabiliriz.
\( (-2, 4) \) aralığı için:
\( f'(x) = -2x + 2 \)
\( f'(2) \) değerini bulmak için \( x = 2 \) koyalım.
\( f'(2) = -2(2) + 2 = -2 \) bulunur.
\( g(x) = \begin{cases} x^3 + ax^2 + 4bx - 5 & x \le -1 \\ -x^2 + bx - 3a & x \gt -1 \end{cases} \)
fonksiyonu her noktada türevlenebilir olduğuna göre, \( a \cdot b \) çarpımı kaçtır?
Çözümü GösterVerilen parçalı fonksiyonun iki aralıktaki tanımı da birer polinom fonksiyonudur. Polinom fonksiyonları tüm reel sayılarda sürekli ve türevlenebilirdir.
Parçalı fonksiyonun her noktada türevlenebilir olması için, geçiş noktası olan \( x = -1 \) noktasında da sürekli olmalıdır.
Fonksiyonun \( x = -1 \) noktasındaki soldan limiti:
\( \lim\limits_{x \to -1^-} g(x) = \lim\limits_{x \to -1^-} (x^3 + ax^2 + 4bx - 5) \)
\( = (-1)^3 + a(-1)^2 + 4b(-1) - 5 \)
\( = a - 4b - 6 \)
Fonksiyonun \( x = -1 \) noktasındaki sağdan limiti:
\( \lim\limits_{x \to -1^+} g(x) = \lim\limits_{x \to -1^+} (-x^2 + bx - 3a) \)
\( = -(-1)^2 + b(-1) - 3a \)
\( = -3a - b - 1 \)
\( x = -1 \) noktasındaki fonksiyon değeri:
\( g(-1) = a - 4b - 6 \)
Fonksiyonun bu noktada sürekli olması için soldan ve sağdan limit değerleri ve fonksiyon değeri bu noktada tanımlı ve birbirine eşit olmalıdır.
\( a - 4b - 6 = -3a - b - 1 \)
\( 4a - 3b = 5 \)
Fonksiyon bu noktada türevlenebilir olduğuna göre soldan ve sağdan türevler tanımlı ve birbirine eşit olmalıdır.
Fonksiyonun türev fonksiyonunu bulalım.
\( g'(x) = \begin{cases} 3x^2 + 2ax + 4b & x \le -1 \\ -2x + b & x \gt -1 \end{cases} \)
Fonksiyonun \( x = -1 \) noktasındaki soldan türevi:
\( g'(-1^-) = 3(-1)^2 + 2a(-1) + 4b \)
\( = -2a + 4b + 3 \)
Fonksiyonun \( x = -1 \) noktasındaki sağdan türevi:
\( g'(-1^+) = -2(-1) + b \)
\( = b + 2 \)
Fonksiyonun bu noktada türevlenebilir olması için soldan ve sağdan türev değerleri tanımlı ve birbirine eşit olmalıdır.
\( -2a + 4b + 3 = b + 2 \)
\( -2a + 3b = -1 \)
Elde ettiğimiz iki bilinmeyenli iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = 2, \quad b = 1 \)
\( a \cdot b = 2 \cdot 1 = 2 \) bulunur.
\( f(x) = \begin{cases} ax^2 + 2 & x \lt -1 \\ 2bx - 1 & x \ge -1 \end{cases} \)
fonksiyonu tüm reel sayılarda türevlenebilir olduğuna göre, \( (a, b) \) ikilisini bulunuz.
Çözümü Göster\( x = -1 \) noktası parçalı fonksiyonun geçiş noktasıdır.
Parçalı fonksiyonun her iki tanımındaki ifadeler birer polinom fonksiyonudur. Polinom fonksiyonları tüm reel sayılarda sürekli ve türevlenebilirdir.
Parçalı fonksiyonun türevsiz olabileceği tek nokta \( x = -1 \) noktasıdır. Fonksiyon tüm reel sayılarda türevlenebilir olduğuna göre bu geçiş noktasında da sürekli olmalıdır.
Önce bu noktadaki soldan ve sağdan limit değerlerini ve fonksiyon değerini bularak bu noktadaki sürekliliği kontrol edelim.
Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
Fonksiyonun \( x = -1 \) noktasındaki soldan limiti:
\( \lim\limits_{x \to -1^-} f(x) = a(-1)^2 + 2 = a + 2 \)
Fonksiyonun \( x = -1 \) noktasındaki sağdan limiti:
\( \lim\limits_{x \to -1^+} f(x) = 2b(-1) - 1 = -2b - 1 \)
\( x = -1 \) noktasındaki fonksiyon değeri:
\( f(-1) = -2b - 1 \)
Fonksiyon bu noktada sürekli olduğuna göre, soldan ve sağdan limit değerleri ve fonksiyon değeri birbirine eşit olmalıdır.
\( a + 2 = -2b - 1 \)
\( a + 2b = -3 \)
Fonksiyon bu noktada türevlenebilir olduğuna göre soldan ve sağdan türevler tanımlı ve birbirine eşit olmalıdır.
\( f'(x) = \begin{cases} 2ax & x \lt -1 \\ 2b & x \ge -1 \end{cases} \)
Fonksiyonun \( x = -1 \) noktasındaki soldan türevi:
\( f'(-1^-) = 2a(-1) = -2a \)
Fonksiyonun \( x = -1 \) noktasındaki sağdan türevi:
\( f'(-1^+) = 2b \)
Fonksiyon bu noktada türevlenebilir olduğuna göre soldan ve sağdan türev değerleri birbirine eşit olmalıdır.
\( -2a = 2b \)
\( a = -b \)
\( a \) ve \( b \) arasında bulduğumuz iki bilinmeyenli iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( (a, b) = (3, -3) \) bulunur.
\( f: \mathbb{R} - \{-2\} \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{\abs{x - 2}}{x + 2} \) fonksiyonunun \( x = 2 \) noktasındaki sürekliliğini ve türevlenebilirliğini inceleyin.
Çözümü GösterFonksiyonu parçalı fonksiyon şeklinde yazalım.
\( x - 2 \) ifadesi \( x \lt 2 \) aralığında negatif olduğu için mutlak değerden negatif işaretli, \( x \ge 2 \) aralığında sıfır ya da pozitif olduğu için olduğu gibi çıkar.
\( f(x) = \begin{cases} \dfrac{-x + 2}{x + 2} & x \lt 2 \\ \dfrac{x - 2}{x + 2} & x \ge 2 \end{cases} \)
Fonksiyonun \( x = 2 \) noktasındaki soldan ve sağdan türevlenebilirliğini türev alma kurallarını kullanarak bulalım.
Türev alma kurallarını kullanmadan önce bu noktadaki sürekliliği kontrol etmemiz gerekir.
Fonksiyonun \( x = 2 \) noktasındaki soldan limiti:
\( \lim\limits_{x \to 2^-} f(x) = \lim\limits_{x \to 2^-} \dfrac{-x + 2}{x + 2} = 0 \)
\( = \dfrac{-2 + 2}{2 + 2} = 0 \)
Fonksiyonun \( x = 2 \) noktasındaki sağdan limiti:
\( \lim\limits_{x \to 2^+} f(x) = \lim\limits_{x \to 2^+} \dfrac{x - 2}{x + 2} = 0 \)
\( = \dfrac{2 - 2}{2 + 2} = 0 \)
\( x = 2 \) noktasındaki fonksiyon değeri:
\( f(2) = \dfrac{2 - 2}{2 + 2} = 0 \)
Buna göre bu noktada soldan ve sağdan limitler ve fonksiyon değeri birer reel sayı olarak tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = 2 \) noktasında süreklidir.
\( f(2^-) = f(2^+) = f(2) \)
Sürekliliğini gösterdiğimiz bu noktadaki türevlenebilirliği kontrol edelim.
Fonksiyonun türev fonksiyonunu bulalım.
\( f'(x) = \begin{cases} \dfrac{-4}{(x + 2)^2} & x \lt 2, \\ \dfrac{4}{(x + 2)^2} & x \ge 2 \end{cases} \)
Fonksiyonun \( x = 2 \) noktasındaki soldan türevi:
\( f'(2^-) = \dfrac{-4}{(2 + 2)^2} = -\dfrac{1}{4} \)
Fonksiyonun \( x = 2 \) noktasındaki sağdan türevi:
\( f'(2^+) = \dfrac{4}{(2 + 2)^2} = \dfrac{1}{4} \)
Fonksiyon \( x = 2 \) noktasında sürekli olsa da, soldan ve sağdan türev değerleri birbirine eşit olmadığı için bu noktada türevlenebilir değildir.
\( f'(2^-) \ne f'(2^+) \)
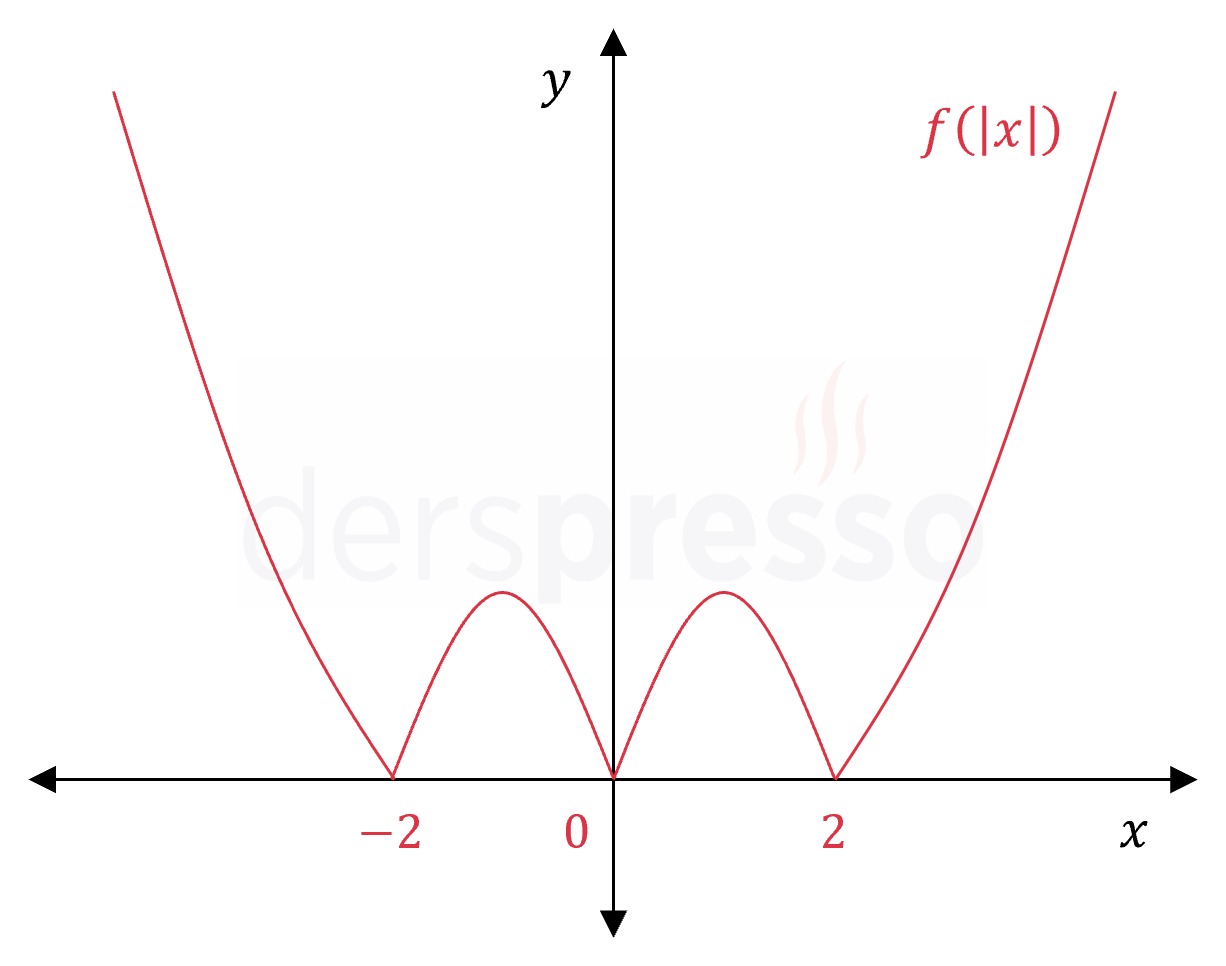
\( f(x) = \abs{x^2 - 2x} \) fonksiyonu veriliyor.
\( f(\abs{x}) \) fonksiyonunun \( x = 0 \) ve \( x = 2 \) noktalarındaki sürekliliğini ve türevlenebilirliğini inceleyin.
Çözümü Göster\( f(x) = \abs{x^2 - 2x} = \abs{x(x - 2)} \)
Fonksiyonu parçalı fonksiyon şeklinde yazalım.
\( x(x - 2) \) ifadesi \( 0 \lt x \lt 2 \) aralığında negatif olduğu için mutlak değerden negatif işaretli, diğer aralıklarda sıfır ya da pozitif olduğu için olduğu gibi çıkar.
\( f(x) = \begin{cases} x^2 - 2x & x \le 0 \\ -x^2 + 2x & 0 \lt x \lt 2 \\ x^2 - 2x & x \ge 2 \end{cases} \)
\( f(\abs{x}) \) fonksiyonunu bulmak için \( f(x) \) tanımında \( x \) yerine \( \abs{x} \) yazalım.
\( f(\abs{x}) = \begin{cases} \abs{x}^2 - 2\abs{x} & \abs{x} \le 0 \\ -\abs{x}^2 + 2\abs{x} & 0 \lt \abs{x} \lt 2 \\ \abs{x}^2 - 2\abs{x} & \abs{x} \ge 2 \end{cases} \)
Mutlak değerli bir ifade negatif olamaz, dolayısıyla parçalı fonksiyonun birinci aralığını tanımdan çıkarabiliriz. \( x = 0 \) değerinde birinci ve ikinci aralık aynı sıfır değerini verdiği için bu değeri ikinci aralığa dahil edebiliriz.
\( f(\abs{x}) = \begin{cases} -\abs{x}^2 + 2\abs{x} & 0 \le \abs{x} \lt 2 \\ \abs{x}^2 - 2\abs{x} & \abs{x} \ge 2 \end{cases} \)
\( 0 \le \abs{x} \lt 2 \) aralığını \( x \) işaretine göre iki aralığa bölelim.
\( -2 \lt x \lt 0 \) ve \( 0 \le x \lt 2 \)
\( -2 \lt x \lt 0 \) ise \( -\abs{x^2} + 2\abs{x} = -x^2 - 2x \)
\( 0 \le x \lt 2 \) ise \( -\abs{x^2} + 2\abs{x} = -x^2 + 2x \)
\( \abs{x} \ge 2 \) aralığını \( x \) işaretine göre iki aralığa bölelim.
\( x \ge 2 \) ve \( x \le -2 \)
\( x \ge 2 \) ise \( \abs{x}^2 - 2\abs{x} = x^2 - 2x \)
\( x \le -2 \) ise \( \abs{x}^2 - 2\abs{x} = x^2 + 2x \)
Buna göre \( f(\abs{x}) \) fonksiyonunun tanımı aşağıdaki gibi olur.
\( f(\abs{x}) = \begin{cases} x^2 + 2x & x \le -2 \\ -x^2 - 2x & -2 \lt x \lt 0 \\ -x^2 + 2x & 0 \le x \lt 2 \\ x^2 - 2x & x \ge 2 \end{cases} \)
Fonksiyonun \( x = 0 \) noktasındaki sürekliliğini inceleyelim.
\( \lim\limits_{x \to 0^-} f(\abs{x}) = \lim\limits_{x \to 0^-} (-x^2 - 2x) = 0 \)
\( \lim\limits_{x \to 0^+} f(\abs{x}) = \lim\limits_{x \to 0^+} (-x^2 + 2x) = 0 \)
\( f(\abs{0}) = -0^2 + 2(0) = 0 \)
Soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olduğu için fonksiyon \( x = 0 \) noktasında süreklidir.
Fonksiyonun \( x = 2 \) noktasındaki sürekliliğini inceleyelim.
\( \lim\limits_{x \to 2^-} f(\abs{x}) = \lim\limits_{x \to 2^-} (-x^2 + 2x) = 0 \)
\( \lim\limits_{x \to 2^+} f(\abs{x}) = \lim\limits_{x \to 2^+} (x^2 - 2x) = 0 \)
\( f(\abs{2}) = 2^2 - 2(2) = 0 \)
Soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olduğu için fonksiyon \( x = 2 \) noktasında süreklidir.
Fonksiyonun türev fonksiyonunu bulalım.
\( f'(\abs{x}) = \begin{cases} 2x + 2 & x \le -2 \\ -2x - 2 & -2 \lt x \lt 0 \\ -2x + 2 & 0 \le x \lt 2 \\ 2x - 2 & x \ge 2 \end{cases} \)
Fonksiyonun \( x = 0 \) noktasındaki türevlenebilirliğini inceleyelim.
\( f'(0^-) = -2(0) - 2 = -2 \)
\( f'(0^+) = -2(0) + 2 = 2 \)
Fonksiyon \( x = 0 \) noktasında sürekli olsa da, soldan ve sağdan türev değerleri birbirine eşit olmadığı için bu noktada türevlenebilir değildir.
Fonksiyonun \( x = 2 \) noktasındaki türevlenebilirliğini inceleyelim.
\( f'(2^-) = -2(2) + 2 = -2 \)
\( f'(2^+) = 2(2) - 2 = 2 \)
Fonksiyon \( x = 2 \) noktasında sürekli olsa da, soldan ve sağdan türev değerleri birbirine eşit olmadığı için bu noktada türevlenebilir değildir.
\( f(\abs{x}) \) fonksiyonunun bu iki noktadaki sürekliliği ve türevlenebilirliği aşağıdaki grafik üzerinde de incelenebilir.