İlişkili Oranlar
\( x \) ve \( y \) değişkenleri arasında \( y = f(x) \) şeklinde bir ilişki tanımlı olsun ve bu değişkenlerin zamana bağlı değişim gösterdiğini varsayalım.
\( y = y(t), \quad x = x(t) \) olmak üzere,
\( y(t) = f(x(t)) \)
Zincir kuralı ile tarafların türevi alındığında değişkenlerin zamana bağlı değişim oranları arasında aşağıdaki ilişki elde edilir.
\( y'(t) = f'(x(t)) \cdot x'(t) \)
\( \dfrac{dy}{dt} = \dfrac{dy}{dx} \cdot \dfrac{dx}{dt} \)
Elde edilen bu denklemde \( \frac{dy}{dt} \) ifadesi \( y \) değişkeninin zamana bağlı anlık değişim oranını, \( \frac{dx}{dt} \) ifadesi de \( x \) değişkeninin zamana bağlı anlık değişim oranını gösterir.
İki ya da daha fazla değişken arasında tanımlı bir denklemin bir bağımsız değişkene göre türevi alındığında değişkenlerin değişim oranları arasında kurulan bu ilişkiye ilişkili oranlar denir.
Değişkenlerin değişim gösterdiği bağımsız değişken çoğu durumda zamandır.
Küre şeklinde bir balona saniyede 800 cm\( ^3 \) hava üfleniyor. Balonun yarıçapı 40 cm olduğu andaki yarıçapın artış hızını bulalım.
Kürenin hacim formülünü yazalım.
\( V = \dfrac{4}{3}\pi r^3 \)
Balonun hacmi ve yarıçapı zamana bağlı değişim gösteren değişkenlerdir.
\( V(t) = \dfrac{4}{3}\pi [r(t)]^3 \)
Bu iki değişkenin zamana bağlı anlık değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dV}{dt} = \dfrac{dV}{dr} \cdot \dfrac{dr}{dt} \)
\( \dfrac{dV}{dt} = 4\pi r^2 \cdot \dfrac{dr}{dt} \)
Elde ettiğimiz bu denklem balonun hacmi ile yarıçapının zamana bağlı anlık değişim oranları arasındaki ilişkiyi vermektedir.
Soruda \( r = 40 \) cm olduğu andaki yarıçapın artış hızı istenmektedir.
\( \dfrac{dr}{dt} = ? \)
Balona havanın üflenme hızı balonun hacminin anlık büyüme hızını verir.
\( \dfrac{dV}{dt} = 800 \) cm\( ^3 \)/sn
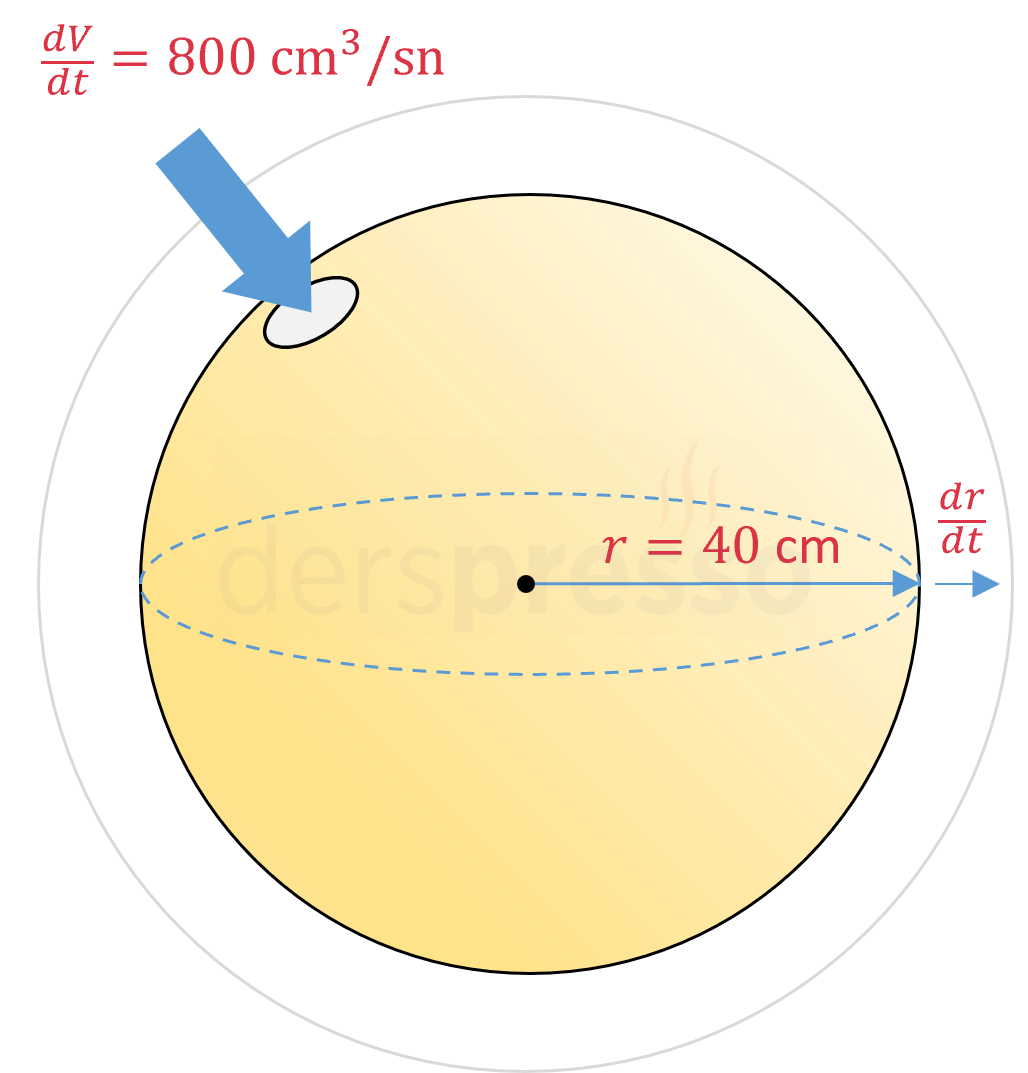
Verilen değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dV}{dt} = 4\pi r^2 \cdot \dfrac{dr}{dt} \)
\( 800 = 4\pi 40^2 \cdot \dfrac{dr}{dt} \)
\( \dfrac{dr}{dt} = \dfrac{1}{8\pi} \) cm/sn
Buna göre \( r = 40 \) cm olduğu anda balonun yarıçapı \( \frac{1}{8\pi} \) cm/sn hızla artmaktadır.
İlişkili oran problemlerinin çözümünde kullanılan yöntem aşağıdaki şekilde özetlenebilir.
- Değişkenlerin anlık değerleri arasındaki ilişki bir denklem şeklinde ifade edilir.
- Zamana bağlı değişen ve sabit olan büyüklükler belirlenir.
- Denklemin iki tarafının zamana bağlı türevi alınarak değişkenlerin anlık değişim oranları arasındaki ilişki elde edilir. Zamana bağlı değişen değişkenlerin türevi alınırken zincir kuralı kullanılır.
- Anlık değerlerden ve anlık değişim oranlarından bilinenler ve hesaplanabilenler denklemde yerine konur ve bilinmeyen değer bulunur.
Bir dikdörtgenin genişliği dakikada 5 cm artmakta, yüksekliği dakikada 2 cm azalmaktadır. Bu dikdörtgenin genişliği 20 cm, yüksekliği 12 cm olduğu andaki alanının değişim hızını bulalım.
Dikdörtgenin genişliğine \( x \), yüksekliğine \( y \) diyelim.
Dikdörtgenin alan formülünü yazalım.
\( A = x \cdot y \)
Dikdörtgenin alanı, genişliği ve yüksekliği zamana bağlı değişim gösteren değişkenlerdir.
\( A(t) = x(t) \cdot y(t) \)
Bu üç değişkenin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( x \) ve \( y \) zamana bağlı değişim gösteren değişkenler oldukları için, çarpımlarının türevini alırken çarpım kuralı kullanılır.
\( \dfrac{dA}{dt} = \dfrac{dx}{dt} \cdot y + x \cdot \dfrac{dy}{dt} \)
Elde ettiğimiz bu denklem dikdörtgenin alanı, yüksekliği ile genişliğinin zamana bağlı anlık değişim oranları arasındaki ilişkiyi vermektedir.
Soruda \( x = 20 \) cm ve \( y = 12 \) cm olduğu anda dikdörtgenin alanının değişim hızı istenmektedir.
\( \dfrac{dA}{dt} = ? \)
Dikdörtgenin genişliği dakikada 5 cm artmakta, yüksekliği dakikada 2 cm azalmaktadır.
\( \dfrac{dx}{dt} = 5 \) cm/dk
\( \dfrac{dy}{dt} = -2 \) cm/dk

Verilen değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dA}{dt} = \dfrac{dx}{dt} \cdot y + x \cdot \dfrac{dy}{dt} \)
\( = 5 \cdot 12 + 20 \cdot (-2) \)
\( = 20 \) cm\( ^2 \)/dk
Buna göre dikdörtgenin alanı belirtilen anda \( 20 \) cm\( ^2 \)/dk hızla artmaktadır.
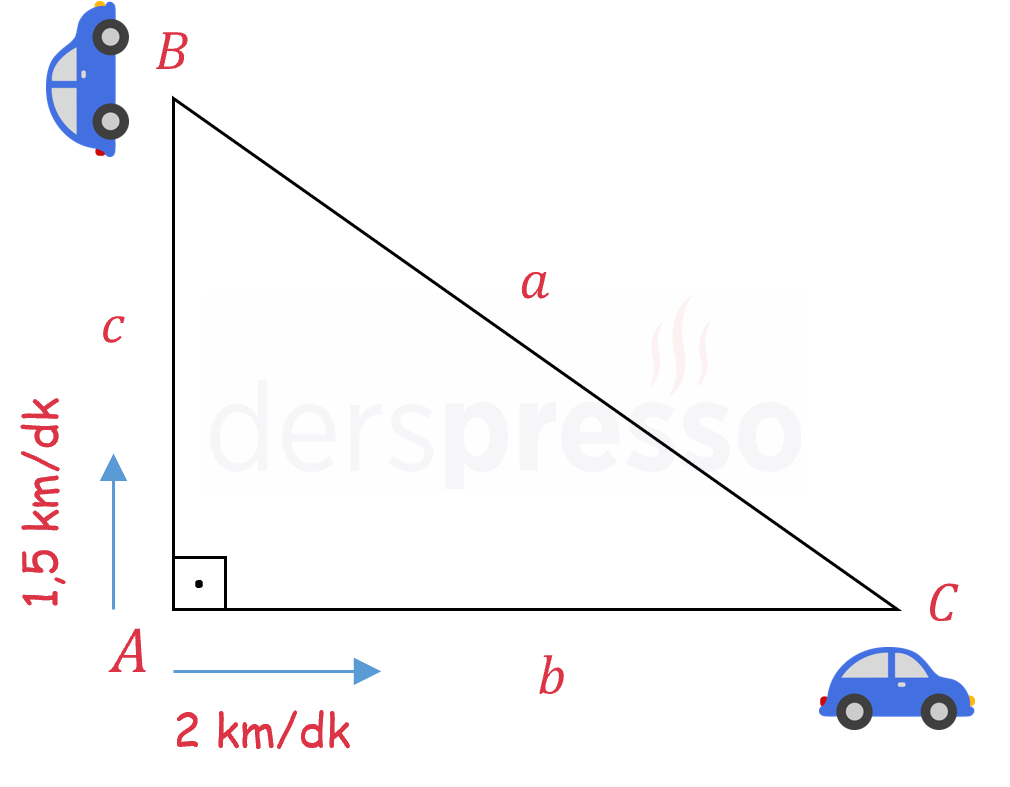
\( A \) noktasında bulunan iki araçtan birincisi 2 km/dk sabit hızla doğu istikametinde, ikincisi 1,5 km/dk sabit hızla kuzey istikametinde hareket ediyor.
Araçlar 20 dakika sonra sırasıyla \( C \) ve \( B \) noktalarında olduğuna göre, bu anda aralarındaki mesafenin artış hızı nedir?
Araçların katettikleri mesafelere sırasıyla \( b \) ve \( c \), herhangi bir anda aralarındaki mesafeye de \( a \) diyelim.
Oluşan dik üçgende Pisagor teoremini kullanarak \( a \) uzunluğunu \( b \) ve \( c \) cinsinden aşağıdaki şekilde yazabiliriz.
\( a^2 = b^2 + c^2 \)
Üç kenar uzunluğu da zamana bağlı değişim gösteren değişkenlerdir.
\( [a(t)]^2 = [b(t)]^2 + [c(t)]^2 \)
Bu üç değişkenin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{d(a^2)}{dt} = \dfrac{d(b^2)}{dt} + \dfrac{d(c^2)}{dt} \)
\( 2a\dfrac{da}{dt} = 2b\dfrac{db}{dt} + 2c\dfrac{dc}{dt} \)
Eşitliğin taraflarını 2'ye bölelim.
\( a\dfrac{da}{dt} = b\dfrac{db}{dt} + c\dfrac{dc}{dt} \)
Elde ettiğimiz bu denklem araçları konumları ile aralarındaki mesafenin anlık değişim oranları arasındaki ilişkiyi vermektedir.
Soruda araçlar \( C \) ve \( B \) noktalarında iken aralarındaki mesafenin artış hızı istenmektedir.
\( \dfrac{da}{dt} = ? \)
Araçların hızı her bir kenarın uzunluğunun anlık artış hızını verir.
\( \dfrac{db}{dt} = 2 \) km/dk
\( \dfrac{dc}{dt} = 1,5 \) km/dk
\( b \) ve \( c \) uzunlukları araçların 20 dk'da katettikleri mesafelere eşittir.
\( b = 20 \cdot 2 = 40 \) km
\( c = 20 \cdot 1,5 = 30 \) km
\( a \) uzunluğunu Pisagor teoremi ile bulabiliriz.
\( a^2 = b^2 + c^2 \)
\( a^2 = 40^2 + 30^2 \)
\( a = 50 \) km
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( a\dfrac{da}{dt} = b\dfrac{db}{dt} + c\dfrac{dc}{dt} \)
\( 50\dfrac{da}{dt} = 40 \cdot 2 + 30 \cdot 1,5 \)
\( \dfrac{da}{dt} = 2,5 \) km/dk
Buna göre araçların arasındaki mesafe belirtilen anda \( 2,5 \) km/dk hızla artmaktadır.
Yukarıdaki 2. örneği dikdörtgenin çevresi için çözünüz.
Bir dikdörtgenin genişliği dakikada 5 cm artmakta, yüksekliği dakikada 2 cm azalmaktadır. Bu dikdörtgenin genişliği 20 cm, yüksekliği 12 cm olduğu andaki çevresinin değişim hızı kaçtır?
Çözümü GösterDikdörtgenin çevre formülünü yazalım.
\( P = 2x + 2y \)
Dikdörtgenin çevresi, genişliği ve yüksekliği zamana bağlı değişim gösteren değişkenlerdir.
\( P(t) = 2x(t) + 2y(t) \)
Bu üç değişkenin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dP}{dt} = 2\dfrac{dx}{dt} + 2\dfrac{dy}{dt} \)
Elde ettiğimiz bu denklem dikdörtgenin çevresi, yüksekliği ile genişliğinin zamana bağlı anlık değişim oranları arasındaki ilişkiyi vermektedir.
Soruda \( x = 20 \) cm ve \( y = 12 \) cm olduğu andaki dikdörtgenin çevresinin değişim hızı istenmektedir.
\( \dfrac{dP}{dt} = ? \)
Dikdörtgenin genişliği dakikada 5 cm artmakta, yüksekliği dakikada 2 cm azalmaktadır.
\( \dfrac{dx}{dt} = 5 \) cm/dk
\( \dfrac{dy}{dt} = -2 \) cm/dk
Verilen değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dP}{dt} = 2\dfrac{dx}{dt} + 2\dfrac{dy}{dt} \)
\( = 2 \cdot 5 + 2 \cdot (-2) \)
\( = 6 \) cm/dk
Buna göre dikdörtgenin çevresi belirtilen anda \( 6 \) cm/dk hızla artmaktadır.
Dikkat edilirse çözümde dikdörtgenin değişim oranlarının sorulduğu andaki genişliğini ve yüksekliğini kullanmamıza gerek kalmadı. Bunun sebebi, çevre ve genişlik/yükseklik değişkenleri arasındaki ilişkinin doğrusal olması ve çevredeki değişim oranının genişlik ve yüksekliğin anlık değerlerine bağlı olmamasıdır.
\( t \) değişkenine bağlı olarak değişen \( x, y, z \) değişkenleri arasındaki ilişki aşağıdaki gibidir.
\( \dfrac{x^5}{20} = y^2 + z^3 \)
\( x \) ve \( y \) değişkenlerinin sabit değişim hızları sırasıyla 5 ve 3 olarak veriliyor.
Buna göre \( x = 2 \) ve \( y = 1 \) için \( \dfrac{dz}{dt} \) kaçtır?
Çözümü GösterEşitliğin iki tarafının \( t \)'ye göre türevini alalım.
\( \dfrac{x^4}{4}\dfrac{dx}{dt} = 2y\dfrac{dy}{dt} + 3z^2\dfrac{dz}{dt} \)
\( x = 2 \) ve \( y = 1 \) için \( z \) değerini bulalım.
\( \dfrac{x^5}{20} = y^2 + z^3 \)
\( \dfrac{2^5}{20} = 1^2 + z^3 \)
\( z^3 = \dfrac{12}{20} = \dfrac{3}{5} \)
\( z = \sqrt[3]{\dfrac{3}{5}} \)
\( x \) ve \( y \) değişkenlerinin sabit değişim hızları sırasıyla 5 ve 3 olarak veriliyor.
\( \dfrac{dx}{dt} = 5, \quad \dfrac{dy}{dt} = 3 \)
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{2^4}{4}(5) = 2(1)(3) + 3(\sqrt[3]{\frac{3}{5}})^2\dfrac{dz}{dt} \)
\( 20 = 6 + 3(\sqrt[3]{\frac{3}{5}})^2\dfrac{dz}{dt} \)
\( \dfrac{dz}{dt} = \dfrac{70\sqrt[3]{\frac{3}{5}}}{9} \) bulunur.
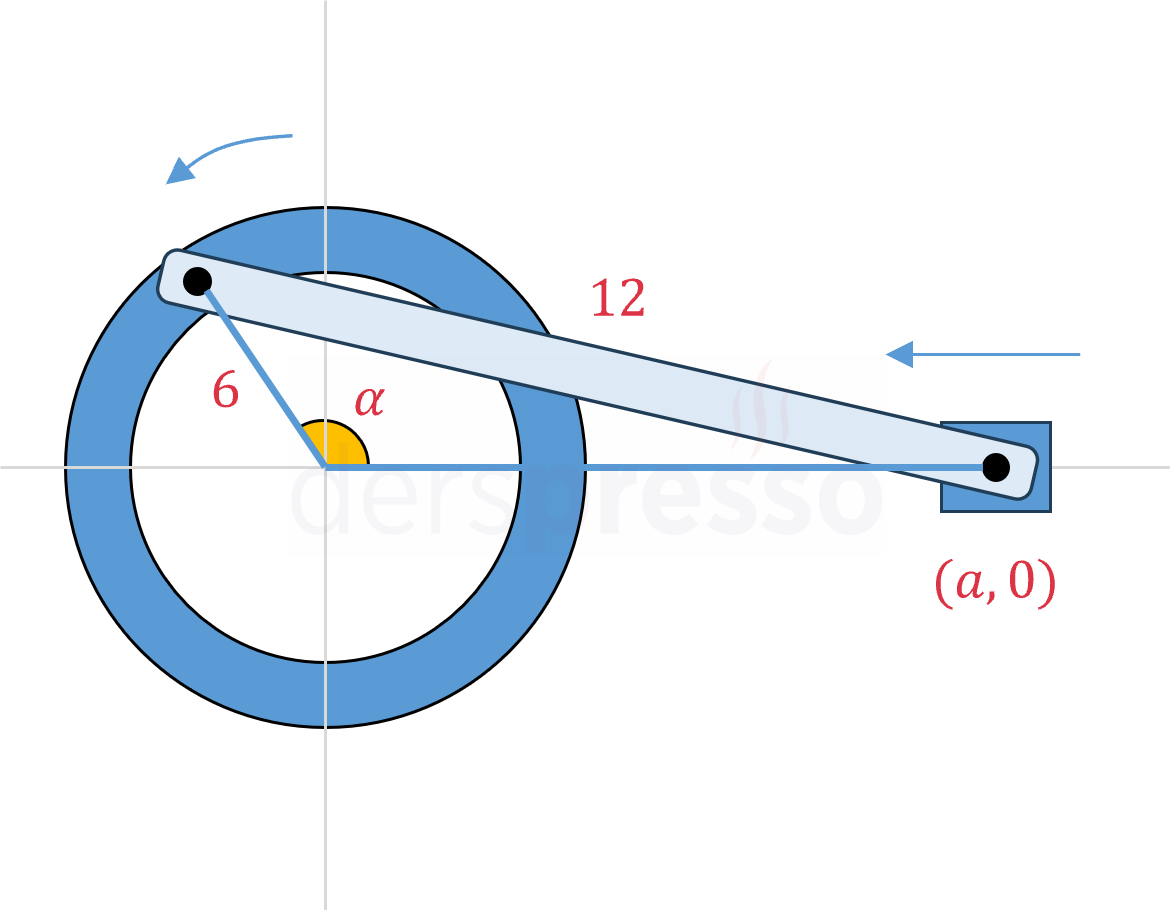
Bir piston yarıçapı 6 cm olan bir krank miline 12 cm uzunluğunda bir çubukla şekilde gösterildiği gibi bağlanmıştır. Piston krank milinin dönme eksenine 10 cm uzaklıkta olduğu anda krank mili saniyede 40 radyan hızla saat yönünün tersine dönmektedir.
Buna göre belirtilen anda pistonun hareket hızı kaçtır?
Çözümü GösterKosinüs teoremini uygulayalım.
\( 12^2 = 6^2 + a^2 - 2(6)(a)\cos{\alpha} \)
\( 144 = 36 + a^2 - 12a\cos{\alpha} \)
Pistonun dönme merkezine uzaklığı ve \( \alpha \) açısı zamana bağlı değişim gösteren değişkenlerdir.
\( 144 = 36 + [a(t)]^2 - 12a(t)\cos(\alpha(t)) \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( 0 = 2a\dfrac{da}{dt} - (12\dfrac{da}{dt}\cos{\alpha} - 12a\sin{\alpha}\dfrac{d\alpha}{dt}) \)
\( 0 = 2a\dfrac{da}{dt} - 12\dfrac{da}{dt}\cos{\alpha} + 12a\sin{\alpha}\dfrac{d\alpha}{dt} \)
Krank milinin dönme eksenine uzaklığı \( a = 10 \) cm olduğu anda pistonun hızı istenmektedir.
\( \dfrac{da}{dt} = ? \)
Belirtilen andaki krank milinin dönme hızı soruda verilmiştir.
Dönme hızı, fiziksel bir terim olarak birim zamanda taranan açı anlamına gelir.
\( \dfrac{d\alpha}{dt} = 40 \) radyan/sn
\( a = 10 \) değerini kosinüs teoreminde yerine koyalım.
\( 144 = 36 + 10^2 - 12(10)\cos{\alpha} \)
\( \cos{\alpha} = -\dfrac{1}{15} \)
\( \alpha \) açısı bir üçgenin iç açısı olduğu için II. bölgede olur. Sinüs fonksiyonu 2. bölgede pozitiftir.
\( \sin{\alpha} = \dfrac{4\sqrt{14}}{15} \)
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( 0 = 2a\dfrac{da}{dt} - 12\dfrac{da}{dt}\cos{\alpha} + 12a\sin{\alpha}\dfrac{d\alpha}{dt} \)
\( 0 = 2(10)\dfrac{da}{dt} - 12\dfrac{da}{dt}(-\dfrac{1}{15}) + 12(10)(\dfrac{4\sqrt{14}}{15})(40) \)
\( 0 = 20\dfrac{da}{dt} + \dfrac{4}{5}\dfrac{da}{dt} + 1280\sqrt{14} \)
\( \dfrac{da}{dt} = -\dfrac{800\sqrt{14}}{13} \) cm/sn
Buna göre piston belirtilen anda saniyede \( \frac{800\sqrt{14}}{13} \) cm hızla krank milinin dönme merkezine yaklaşmaktadır.
Bir kürenin hacmi zamana bağlı olarak artmaktadır. Kürenin hacminin artış hızının yarıçapının artış hızına oranı \( \frac{16\pi}{9} \) cm\( ^2 \) olduğu anda kürenin yarıçapı kaçtır?
Çözümü GösterKürenin hacim formülünü yazalım.
\( V = \dfrac{4}{3}\pi r^3 \)
Kürenin hacmi ve yarıçapı zamana bağlı değişim gösteren değişkenlerdir.
\( V(t) = \dfrac{4}{3}\pi [r(t)]^3 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dV}{dt} = 4\pi r^2\dfrac{dr}{dt} \)
Kürenin hacminin artış hızının yarıçapının artış hızına oranını alalım.
\( \dfrac{\frac{dV}{dt}}{\frac{dr}{dt}} = 4\pi r^2 \)
Kürenin hacminin artış hızının yarıçapının artış hızına oranı soruda verilmiştir.
\( \dfrac{\frac{dV}{dt}}{\frac{dr}{dt}} = \dfrac{16\pi}{9} \)
\( \dfrac{16\pi}{9} = 4\pi r^2 \)
\( r^2 = \dfrac{4}{9} \)
Yarıçap uzunluğu negatif değer alamaz.
\( r = \dfrac{2}{3} \) cm
Buna göre belirtilen anda kürenin yarıçapı \( r = \frac{2}{3} \) cm uzunluğundadır.
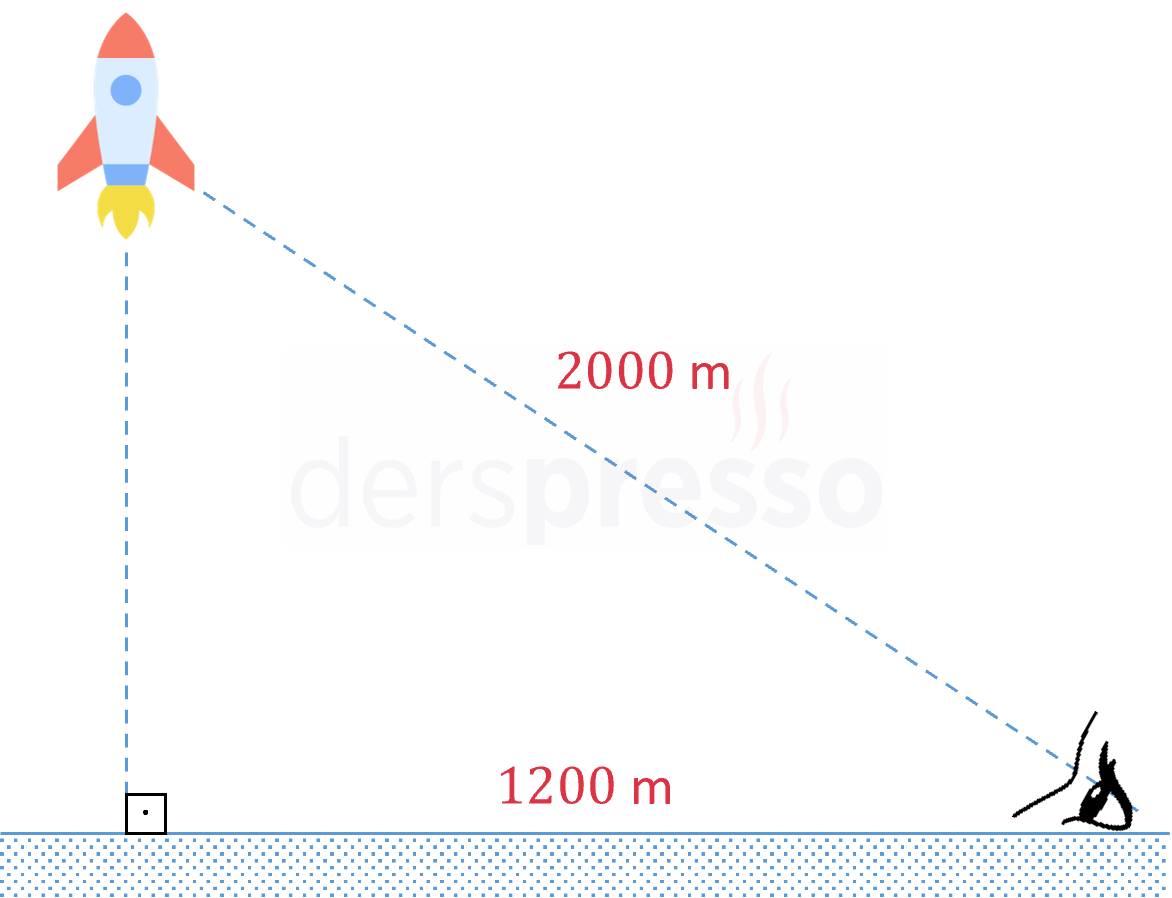
Bir roket dikey olarak fırlatılıyor. Roketin yükselmeye devam ettiği bir anda roket, fırlatma noktasından 1200 metre uzaklıktaki bir gözlemciye 2000 metre uzaklıktadır. Roket ile gözlemci arasındaki uzaklık belirtilen anda saniyede 200 metre hızla artmaktadır.
Buna göre roketin belirtilen andaki dikey hızı kaçtır?
Çözümü GösterRoketin bulunduğu yüksekliğe \( h \), gözlemcinin rokete uzaklığına \( z \) diyelim.
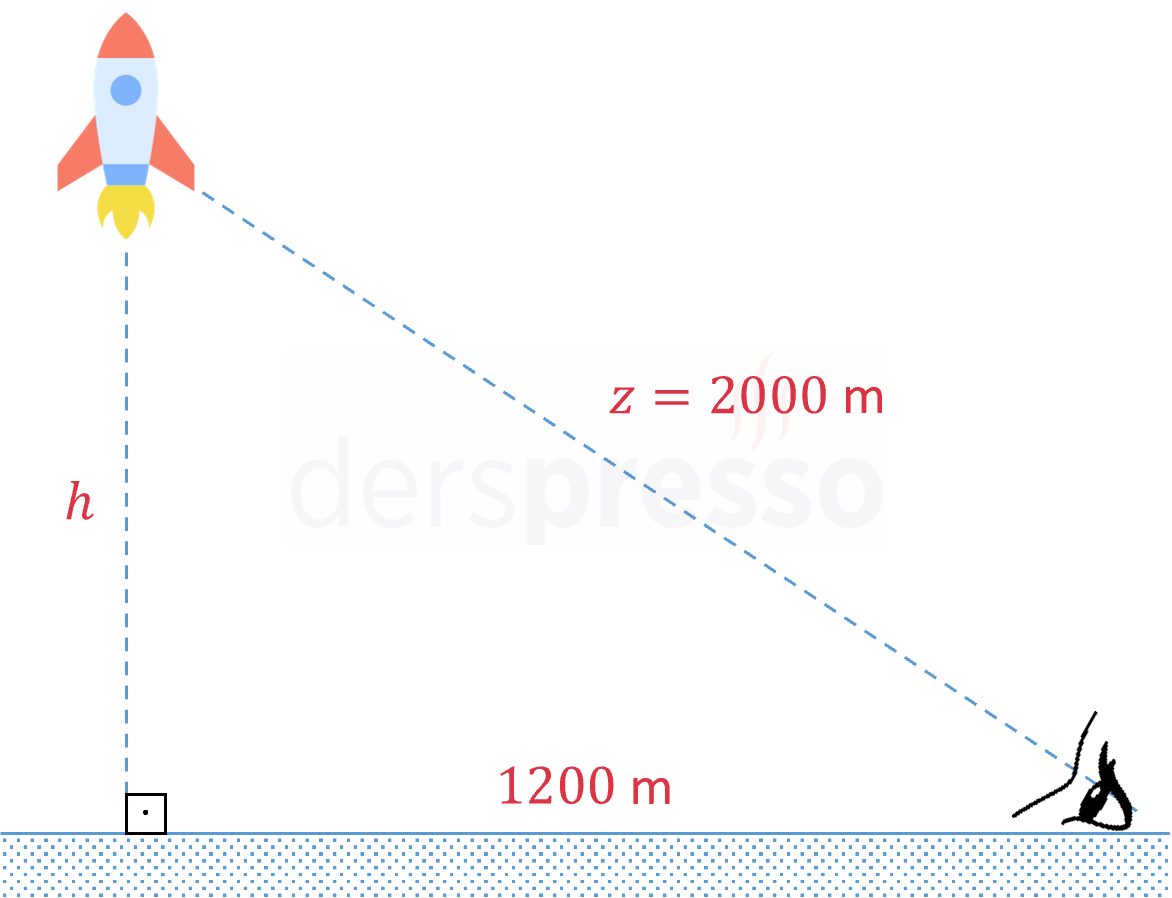
Fırlatma noktası, roket ve gözlemcinin oluşturduğu dik üçgende Pisagor teoremini uygulayalım.
\( z^2 = h^2 + 1200^2 \)
Uçağın yüksekliği ve roket ile gözlemci arasındaki mesafe zamana bağlı değişim gösteren değişkenlerdir.
\( [z(t)]^2 = [h(t)]^2 + 1200^2 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( 2z\dfrac{dz}{dt} = 2h\dfrac{dh}{dt} + 0 \)
\( z\dfrac{dz}{dt} = h\dfrac{dh}{dt} \)
\( z = 2000 \) m olduğu andaki roketin dikey hızı istenmektedir.
\( \dfrac{dh}{dt} = ? \)
\( z \) değerini Pisagor teoreminde yerine koyarak bu andaki \( h \) değerini bulalım.
\( 2000^2 = h^2 + 1200^2 \)
\( h = 1600 \) m
Belirtilen anda roket ile gözlemci arasındaki uzaklığın değişim hızı soruda verilmiştir.
\( \dfrac{dz}{dt} = 200 \) m/sn
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( z\dfrac{dz}{dt} = h\dfrac{dh}{dt} \)
\( 2000(200) = 1600\dfrac{dh}{dt} \)
\( \dfrac{dh}{dt} = 250 \) m/sn
Buna göre belirtilen anda roketin yükselme hızı saniyede 250 metredir.
\( x, y, t \) değişkenleri arasındaki ilişki aşağıdaki iki denklemde verilmiştir.
\( 2y = \dfrac{2}{(x + 1)^3} - \dfrac{1}{2} \)
\( \ln(2x^2) = \dfrac{t}{2} \)
Buna göre, \( x = 1 \) için \( \frac{dy}{dt} \) türevinin değeri kaçtır?
Çözümü GösterZincir kuralını uygulayalım.
\( \dfrac{dy}{dt} = \dfrac{dy}{dx} \cdot \dfrac{dx}{dt} \)
Verilen birinci eşitliğin iki tarafının \( x \)'e göre türevini alalım.
Türevi alırken \( y \) değişkeninin \( x \)'e bağlı bir fonksiyon olduğunu dikkate almalıyız.
\( \dfrac{d}{dx}(2y) = \dfrac{d}{dx}(\dfrac{2}{(x + 1)^3} - \dfrac{1}{2}) \)
\( 2\dfrac{dy}{dx} = -\dfrac{6}{(x + 1)^4} \)
\( \frac{dy}{dx} \) ifadesini yalnız bırakalım.
\( \dfrac{dy}{dx} = -\dfrac{3}{(x + 1)^4} \)
Verilen ikinci eşitliğin iki tarafının \( t \)'ye göre türevini alalım.
Türevi alırken \( x \) değişkeninin \( t \)'ye bağlı bir fonksiyon olduğunu dikkate almalıyız.
\( \dfrac{d}{dt}(\ln(2x^2)) = \dfrac{d}{dt}(\dfrac{t}{2}) \)
\( \dfrac{(2x^2)'}{2x^2} = \dfrac{1}{2} \)
\( \dfrac{4x}{2x^2}\dfrac{dx}{dt} = \dfrac{1}{2} \)
\( \frac{dx}{dt} \) ifadesini yalnız bırakalım.
\( \dfrac{dx}{dt} = \dfrac{x}{4} \)
Bulduğumuz ifadeleri zincir kuralı formülünde yerine koyalım.
\( \dfrac{dy}{dt} = \dfrac{dy}{dx} \cdot \dfrac{dx}{dt} \)
\( = -\dfrac{3}{(x + 1)^4} \cdot \dfrac{x}{4} \)
\( = -\dfrac{3x}{4(x + 1)^4} \)
\( x = 1 \) için türev değerini bulalım.
\( \dfrac{dy}{dt}|_{x=1} = -\dfrac{3(1)}{4(1 + 1)^4} \)
\( = -\dfrac{3}{64} \) bulunur.
\( x, y, t \) değişkenleri arasındaki ilişki aşağıdaki iki denklemde verilmiştir.
\( \dfrac{y}{3} = 30e^{\frac{1}{3} + \frac{x}{10}} \)
\( \dfrac{x}{2} = 6\sqrt{t + 2} \)
Buna göre, \( t = 2 \) için \( \frac{dy}{dt} \) türevinin değeri kaçtır?
Çözümü GösterZincir kuralını uygulayalım.
\( \dfrac{dy}{dt} = \dfrac{dy}{dx} \cdot \dfrac{dx}{dt} \)
Verilen birinci eşitliğin iki tarafının \( x \)'e göre türevini alalım.
Türevi alırken \( y \) değişkeninin \( x \)'e bağlı bir fonksiyon olduğunu dikkate almalıyız.
\( \dfrac{d}{dx}(\dfrac{y}{3}) = \dfrac{d}{dx}(30e^{\frac{1}{3} + \frac{x}{10}}) \)
\( \dfrac{1}{3}\dfrac{dy}{dx} = 30e^{\frac{1}{3} + \frac{x}{10}}\dfrac{1}{10} \)
\( \frac{dy}{dx} \) ifadesini yalnız bırakalım.
\( \dfrac{dy}{dx} = 9e^{\frac{1}{3} + \frac{x}{10}} \)
Verilen ikinci eşitliğin iki tarafının \( t \)'ye göre türevini alalım.
Türevi alırken \( x \) değişkeninin \( t \)'ye bağlı bir fonksiyon olduğunu dikkate almalıyız.
\( \dfrac{d}{dt}(\dfrac{x}{2}) = \dfrac{d}{dt}(6\sqrt{t + 2}) \)
\( \dfrac{1}{2}\dfrac{dx}{dt} = \dfrac{3}{\sqrt{t + 2}} \)
\( \frac{dx}{dt} \) ifadesini yalnız bırakalım.
\( \dfrac{dx}{dt} = \dfrac{6}{\sqrt{t + 2}} \)
Bulduğumuz ifadeleri zincir kuralı formülünde yerine koyalım.
\( \dfrac{dy}{dt} = \dfrac{dy}{dx} \cdot \dfrac{dx}{dt} \)
\( = 9e^{\frac{1}{3} + \frac{x}{10}}\dfrac{6}{\sqrt{t + 2}} \)
\( = \dfrac{54e^{\frac{1}{3} + \frac{x}{10}}}{\sqrt{t + 2}} \)
İkinci eşitliği kullanarak \( t = 2 \) için \( x \) değerini bulalım.
\( \dfrac{x}{2} = 6\sqrt{t + 2} \)
\( \dfrac{x}{2} = 6\sqrt{2 + 2} \)
\( x = 24 \)
Türev denklemini kullanarak \( t = 2 \) ve \( x = 24 \) için \( \frac{dy}{dt} \) değerini bulalım.
\( \dfrac{dy}{dt}|_{t=2, x=24} = \dfrac{54e^{\frac{1}{3} + \frac{24}{10}}}{\sqrt{2 + 2}} \)
\( = 27e^{\frac{41}{15}} \)
Buna göre \( t = 2 \) için \( \frac{dy}{dt} \) değeri \( 27e^{\frac{41}{15}} \) olarak bulunur.
Bir parçacık \( y = \frac{2x^3}{3} + 1 \) grafiği üzerinde ilerlemektedir.
Hangi noktalarda parçacığın \( y \) koordinatının değişim hızı \( x \) koordinatının değişim hızının 18 katıdır?
Çözümü Göster\( x \) ve \( y \) zamana bağlı değişim gösteren değişkenlerdir.
\( y(t) = \dfrac{2[x(t)]^3}{3} + 1 \)
Bu değişkenlerinn zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dy}{dt} = 2x^2\dfrac{dx}{dt} \)
Soruda parçacığın \( y \) koordinatının değişim hızının \( x \) koordinatının değişim hızının 18 katı olduğu noktalar istenmektedir.
\( \dfrac{dy}{dt} = 18\dfrac{dx}{dt} \)
\( \frac{dy}{dt} \) ifadesini ilişkili oran denkleminde \( \frac{dx}{dt} \) cinsinden yazalım.
\( 18\dfrac{dx}{dt} = 2x^2\dfrac{dx}{dt} \)
\( 9 = x^2 \)
\( x = 3 \) ya da \( x = -3 \)
\( x \) değerlerini grafik denkleminde yerine koyalım.
\( x = 3 \) için:
\( y = \dfrac{2(3)^3}{3} + 1 = 19 \)
\( x = -3 \) için:
\( y = \dfrac{2(-3)^3}{3} + 1 = -17 \)
Buna göre \( (3, 19) \) ve \( (-3, -17) \) noktalarında parçacığın \( y \) koordinatının değişim hızı \( x \) koordinatının değişim hızının 18 katıdır.
Bir parçacık \( y = 5x^2 + 2x + 1 \) grafiği üzerinde ilerlemektedir.
Parçacık grafik üzerinde \( x = 2 \) noktasında olduğu anda parçacığın \( x \) koordinatı saniyede 5 birim hızla arttığına göre, bu anda \( y \) koordinatının değişim hızı kaçtır?
Çözümü Göster\( x \) ve \( y \) zamana bağlı değişim gösteren değişkenlerdir.
\( y(t) = 5[x(t)]^2 + 2x(t) + 1 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dy}{dt} = 10x\dfrac{dx}{dt} + 2\dfrac{dx}{dt} \)
\( = \dfrac{dx}{dt}(10x + 2) \)
Parçacık \( x = 2 \) noktasında iken \( x \) koordinatının değişim hızı soruda verilmiştir.
\( \dfrac{dx}{dt} = 5 \) birim/sn
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dy}{dt} = 5(10(2) + 2) \)
\( \dfrac{dy}{dt} = 110 \) birim/sn olarak bulunur.
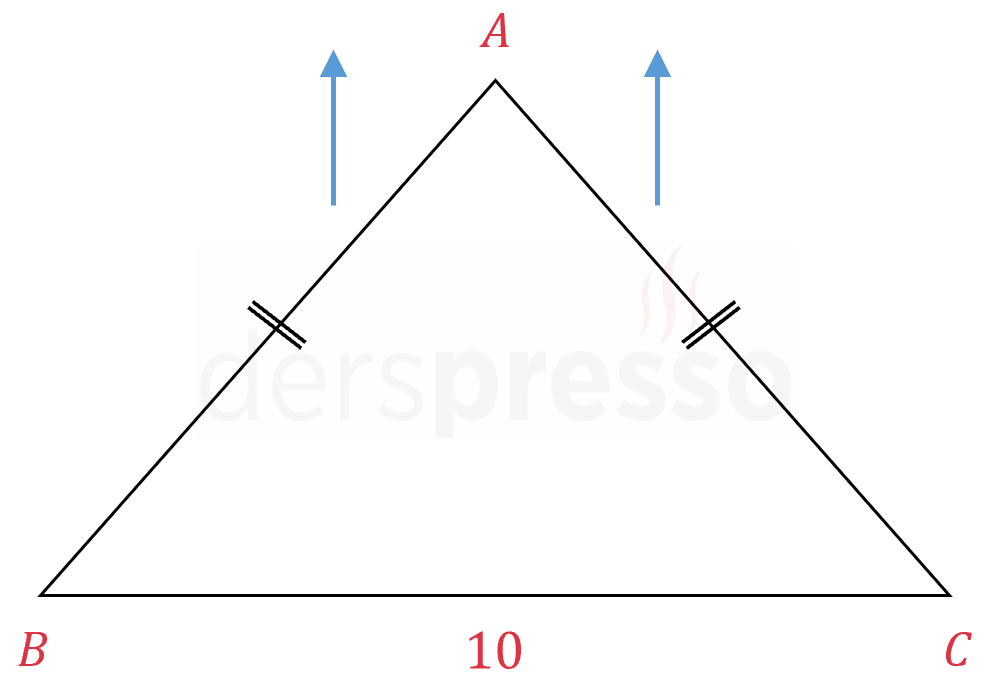
Tabanı 10 cm olan bir ikizkenar üçgende eşit kenarların her biri saniyede 2 cm uzamaktadır.
Bu üçgen eşkenar üçgen olduğu anda üçgenin alanı saniyede kaç cm\( ^2 \) artmaktadır?
Çözümü GösterÜçgenin eşit kenarlarının uzunluğuna \( x \), tabana ait yüksekliğine \( h \) diyelim.
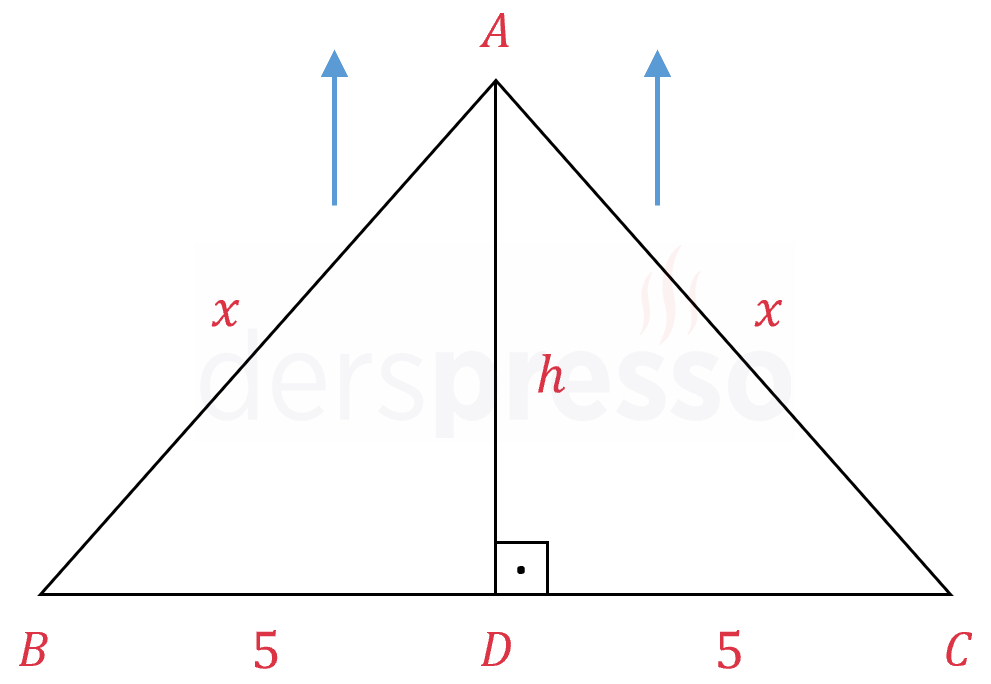
Bir ikizkenar üçgende tabana indirilen yükseklik tabanı ortalar.
\( \abs{BD} = \abs{DC} = 5 \)
Pisagor teoremini kullanarak \( h \) değerini \( x \) cinsinden yazalım.
\( h^2 + 5^2 = x^2 \)
\( h^2 = x^2 - 25 \)
\( h = \sqrt{x^2 - 25} \)
Üçgenin alan formülünü yazalım.
\( A = \dfrac{10h}{2} = 5h \)
\( h \) yerine \( x \) karşılığını yazdığımızda sadece \( x \) değişkenine bağlı olan alan formülünü buluruz.
\( = 5\sqrt{x^2 - 25} \)
Alanın zamana bağlı değişim hızı \( \frac{dA}{dt} \) şeklinde ifade edilir.
Bulduğumuz alan formülü \( x \)'e bağlı olduğu için zincir kuralını kullanarak \( \frac{dA}{dt} \) değişim hızını \( \frac{dA}{dx} \) cinsinden ifade edelim.
\( \dfrac{dA}{dt} = \dfrac{dA}{dx} \cdot \dfrac{dx}{dt} \)
Eşit kenarların saniyedeki büyüme hızı soruda verilmiştir.
\( \dfrac{dx}{dt} = 2 \) cm/sn
\( \dfrac{dA}{dx} \) ifadesini bulmak için alanın \( x \)'e göre türevini alalım.
\( \dfrac{dA}{dx} = \dfrac{5(2x)}{2\sqrt{x^2 - 25}} = \dfrac{5x}{\sqrt{x^2 - 25}} \)
\( \dfrac{dA}{dt} = \dfrac{5x}{\sqrt{x^2 - 25}} \cdot 2 = \dfrac{10x}{\sqrt{x^2 - 25}} \)
Soruda üçgenin eşkenar üçgen olduğu, yani \( x = 10 \) olduğu andaki \( \frac{dA}{dt} \) değeri istenmektedir.
\( \dfrac{dA}{dt}|_{x=10} = \dfrac{10(10)}{\sqrt{10^2 - 25}} = \dfrac{100}{\sqrt{75}} \)
\( = \dfrac{100}{5\sqrt{3}} = \dfrac{20\sqrt{3}}{3} \)
Buna göre ikizkenar üçgen eşkenar üçgen olduğu anda üçgenin alanı saniyede \( \frac{20\sqrt{3}}{3} \) hızla artmaktadır.
Bir parçacık \( y = \sin(2x) \) grafiği üzerinde hareket etmektedir. Grafiğin hangi noktalarında parçacığın \( x \) ve \( y \) koordinatlarının değişim oranı aynıdır?
Çözümü Göster\( x \) ve \( y \) zamana bağlı değişim gösteren değişkenlerdir.
\( y(t) = \sin(2x(t)) \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dy}{dt} = 2\cos(2x)\dfrac{dx}{dt} \)
\( y \) koordinatındaki anlık değişimin \( x \) koordinatındaki anlık değişime oranını alalım.
\( \dfrac{\frac{dy}{dt}}{\frac{dx}{dt}} = 2\cos(2x) \)
Soruda \( y \) koordinatının değişim hızının \( x \) koordinatının değişim hızına eşit olduğu noktalar istenmektedir.
\( \dfrac{dy}{dt} = \dfrac{dx}{dt}\)
\( \dfrac{\frac{dy}{dt}}{\frac{dx}{dt}} = 1 \)
\( \cos(2x) = \dfrac{1}{2} \)
Kosinüs fonksiyonu \( [0, 2\pi] \) aralığında \( x = \frac{\pi}{3} \) ve \( x = \frac{5\pi}{3} \) noktalarında \( \frac{1}{2} \) değerini alır.
Bu iki değer için denklemin genel çözümünü bulalım.
Durum 1: \( x = \frac{\pi}{3} \)
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x = \frac{\pi}{3} + 2\pi k \)
\( x = \frac{\pi}{6} + \pi k \)
Durum 2: \( x = \frac{5\pi}{3} \)
\( 2x = \frac{5\pi}{3} + 2\pi k \)
\( x = \frac{5\pi}{6} + \pi k \)
Buna göre yukarıda bulduğumuz iki çözüm kümesinin birleşimi, parçacığın \( x \) ve \( y \) koordinatlarının aynı oranda değiştiği noktaları içerir.
Bir parçacık \( y = f(x) \) grafiği üzerinde hareket etmektedir. Eğrinin eğiminin \( \frac{2}{3} \) olduğu bir noktada parçacığın \( y \) koordinatının değişim hızı saniyede 4 birim olduğuna göre, parçacığın bu noktada \( x \) koordinatının değişim hızı kaçtır?
Çözümü GösterParçacığın \( x \) ve \( y \) koordinatları zamana bağlı değişim gösteren değişkenlerdir.
\( y(t) = f(x(t)) \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dy}{dt} = f'(x)\dfrac{dx}{dt} \)
\( f'(x) \) eğim fonksiyonudur ve belirtilen anda eğrinin eğimi soruda verilmiştir.
\( f'(x) = \dfrac{2}{3} \)
Belirtilen anda parçacığın \( y \) koordinatının değişim hızı soruda verilmiştir.
\( \dfrac{dy}{dt} = 4 \)
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dy}{dt} = f'(x)\dfrac{dx}{dt} \)
\( 4 = \dfrac{2}{3}\dfrac{dx}{dt} \)
\( \dfrac{dx}{dt} = 6 \) birim/sn
Buna göre belirtilen anda parçacığın \( x \) koordinatının değişim hızı saniyede 6 birimdir.
Bir balon 3 m\( ^3 \)/s hızla hava kaçırmaya başlıyor. Balonun yarıçapı \( \frac{1}{2} \) m olduğu anda balonun yarıçapının değişim hızı kaçtır? (Balon her zaman küre şeklinde kalmaktadır.)
Çözümü GösterKürenin hacim formülünü yazalım.
\( V = \dfrac{4}{3}\pi r^3 \)
Balonun hacmi ve yarıçap uzunluğu zamana bağlı değişim gösteren değişkenlerdir.
\( V(t) = \dfrac{4}{3}\pi [r(t)]^3 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dV}{dt} = 4\pi r^2\dfrac{dr}{dt} \)
Havanın balondan kaçış hızı soruda verilmiştir.
\( \dfrac{dV}{dt} = -3 \) m\( ^3 \)/s
\( r = \frac{1}{2} \) olduğu andaki balonun yarıçapının artış hızı istenmektedir.
\( \dfrac{dr}{dt} = ? \)
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine yazalım.
\( \dfrac{dV}{dt} = 4\pi r^2\dfrac{dr}{dt} \)
\( -3 = 4\pi (\dfrac{1}{2})^2\dfrac{dr}{dt} \)
\( \dfrac{dr}{dt} = -\dfrac{3}{\pi} \) m/s
Buna göre belirtilen anda balonun yarıçapı \( \frac{3}{\pi} \) m/s hızla azalmaktadır.
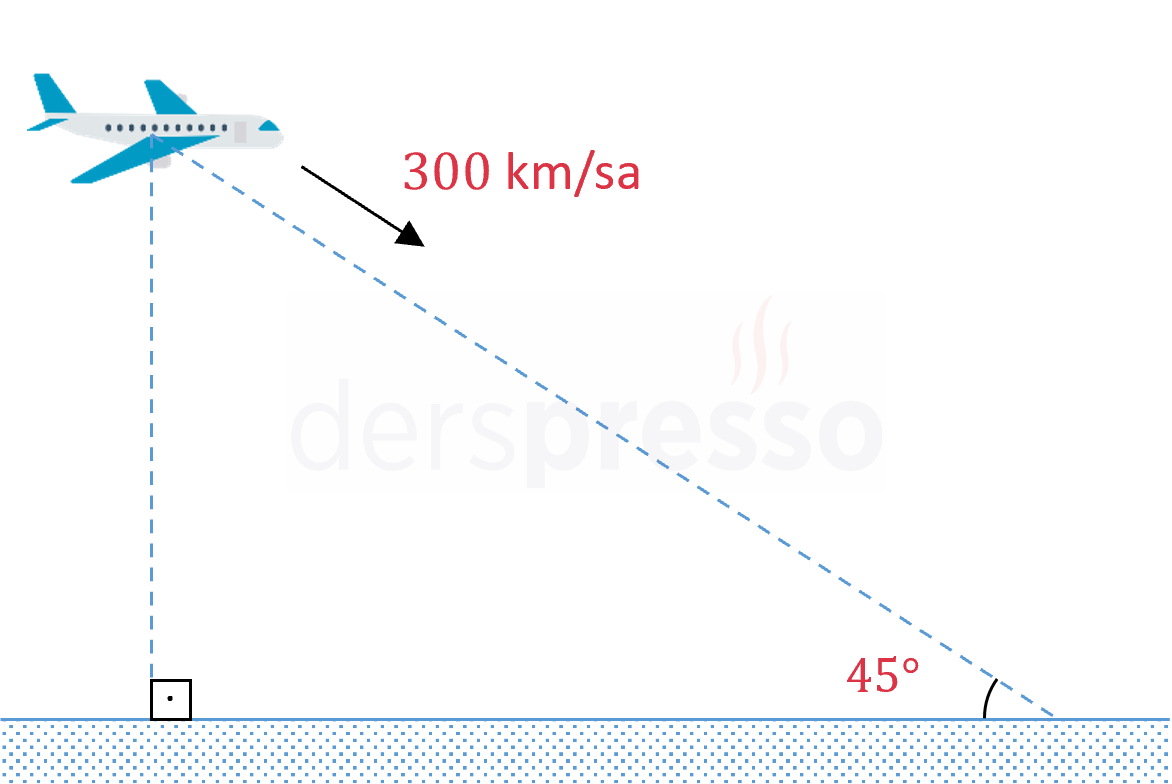
İnişe geçen bir uçak yerle 45° açı yapan bir doğru boyunca saatte 300 km hızla piste yaklaşmaktadır.
Bu uçağın yerden yüksekliğinin değişim hızı kaçtır?
Çözümü GösterUçağın yüksekliğine \( h \), uçuş yönünde yere uzaklığına \( d \) diyelim.
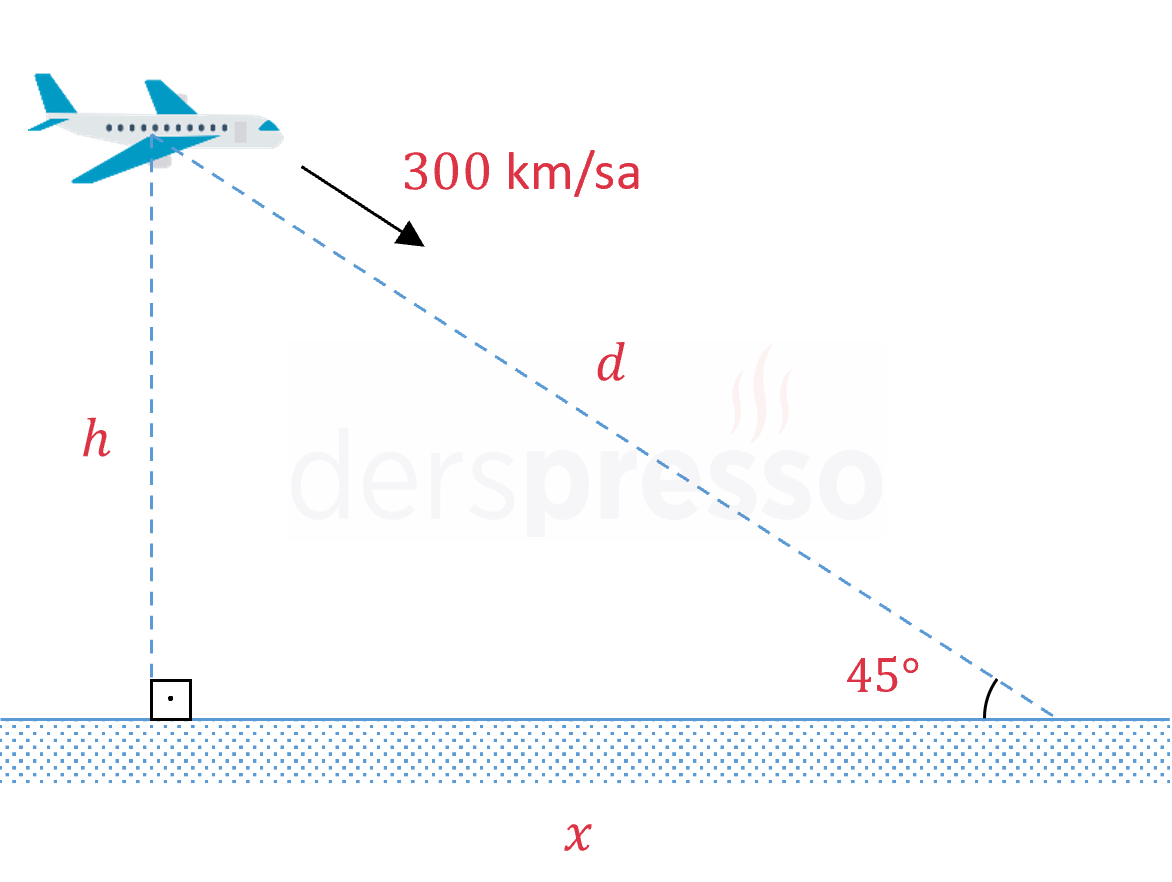
\( \dfrac{h}{d} = \sin{45°} \)
\( \dfrac{h}{d} = \dfrac{\sqrt{2}}{2} \)
İçler - dışlar çarpımı yapalım.
\( 2h = \sqrt{2}d \)
Uçağın yerden yüksekliği ve uçuş rotası boyunca yere olan uzaklığı zamana bağlı değişim gösteren değişkenlerdir.
\( 2h(t) = \sqrt{2}d(t) \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( 2\dfrac{dh}{dt} = \sqrt{2}\dfrac{dd}{dt} \)
Uçağın hızı (yere olan uzaklığındaki değişim hızı) soruda verilmiştir.
\( \dfrac{dd}{dt} = -300 \) km/sa
Verilen değeri ilişkili oran denkleminde yerine koyalım.
\( 2\dfrac{dh}{dt} = \sqrt{2}(-300) \)
\( \dfrac{dh}{dt} = -150\sqrt{2} \)
Buna göre uçağın yerden yüksekliği saatte \( 150\sqrt{2} \) km hızla azalmaktadır.
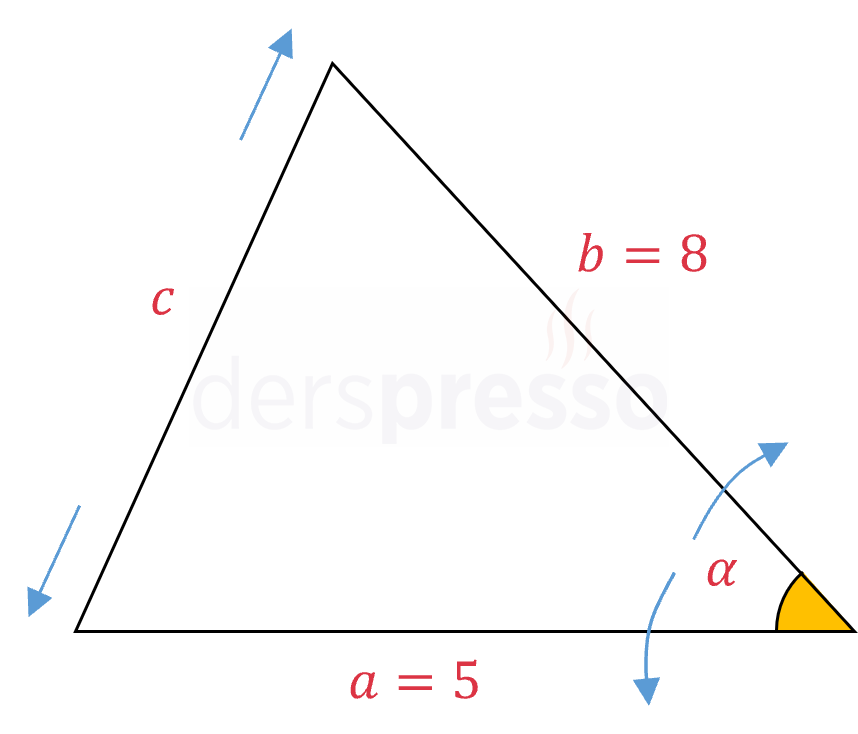
Bir üçgenin iki kenarının uzunluğu 5 cm ve 8 cm'dir. Bu iki kenar arasındaki açı saniyede \( 2° \) hızla artırılmaktadır.
Kenarlar arasındaki açı \( 60° \) olduğu anda, üçüncü (karşı) kenar uzunluğunun artış hızı kaç cm/sn olur?
Çözümü GösterÜçgenin kenar uzunlukları arasındaki ilişkiyi kosinüs teoremi ile kurabiliriz.
\( c^2 = a^2 + b^2 - 2ab\cos{\alpha} \)
Karşı kenar uzunluğu ve \( \alpha \) açısı zamana bağlı değişim gösteren değişkenlerdir. \( a \) ve \( b \) kenar uzunlukları ise sabittir.
\( [c(t)]^2 = a^2 + b^2 - 2ab\cos{\alpha(t)} \)
Bu iki değişkenin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{d(c^2)}{dt} = \dfrac{d(a^2)}{dt} + \dfrac{d(b^2)}{dt} - \dfrac{d(2ab\cos{\alpha})}{dt} \)
\( a \) ve \( b \) birer sabit olduğu için türevleri sıfırdır.
\( 2c\dfrac{dc}{dt} = -2ab(-\sin{\alpha})\dfrac{d\alpha}{dt} \)
\( c\dfrac{dc}{dt} = ab\sin{\alpha}\dfrac{d\alpha}{dt} \)
Elde ettiğimiz bu denklem üçgenin kenar uzunlukları ile \( \alpha \) açısının zamana bağlı anlık değişim oranları arasındaki ilişkiyi vermektedir.
Soruda \( \alpha = 60° \) olduğu andaki \( c \) kenar uzunluğunun artış hızı istenmektedir.
\( \dfrac{dc}{dt} = ? \)
\( \alpha \) açısının artış hızı soruda verilmiştir.
\( \dfrac{d\alpha}{dt} = 2° \) /sn
\( c \) kenar uzunluğunun anlık değerini kosinüs teoremi ile hesaplayabiliriz.
\( c^2 = a^2 + b^2 - 2ab\cos{\alpha} \)
\( c^2 = 5^2 + 8^2 - 2 \cdot 5 \cdot 8 \cdot \cos{60°} \)
\( c^2 = 25 + 64 - 40 \)
\( c = 7 \) cm
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( c\dfrac{dc}{dt} = ab\sin{\alpha}\dfrac{d\alpha}{dt} \)
\( 7\dfrac{dc}{dt} = 5 \cdot 8 \cdot \sin{60°} \cdot 2 \)
\( \dfrac{dc}{dt} = \dfrac{40\sqrt{3}}{7} \) cm/sn
Buna göre karşı kenar uzunluğu belirtilen anda \( \frac{40\sqrt{3}}{7} \) cm/sn hızla artmaktadır.
Bir kürenin yarıçapı saniyede \( \frac{2}{\sqrt{\pi}} \) cm sabit hızla artmaktadır. Kürenin yüzey alanı 100 cm\( ^2 \) olduğu anda kürenin yüzey alanının artış hızı kaç cm\( ^2 \)/sn olur?
Çözümü GösterKürenin yüzey alan formülünü yazalım.
\( A = 4\pi r^2 \)
Kürenin yüzey alanı ve yarıçapı zamana bağlı değişim gösteren değişkenlerdir.
\( A(t) = 4\pi [r(t)]^2 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dA}{dt} = 8\pi r\dfrac{dr}{dt} \)
Elde ettiğimiz bu denklem kürenin yüzey alanı ile yarıçapının zamana bağlı anlık değişim oranları arasındaki ilişkiyi vermektedir.
Kürenin yarıçapının artış hızı soruda verilmiştir.
\( \dfrac{dr}{dt} = \dfrac{2}{\sqrt{\pi}} \) cm/sn
\( A = 100 \) cm\( ^2 \) olduğu andaki kürenin yüzey alanının artış hızı istenmektedir.
\( \dfrac{dA}{dt} = ? \)
Kürenin yüzey alan formülünü kullanarak bu \( A \) değerindeki yarıçap değerini bulalım.
\( A = 4\pi r^2 \)
\( 100 = 4\pi r^2 \)
\( r = \dfrac{5}{\sqrt{\pi}} \) cm
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dA}{dt} = 8\pi r\dfrac{dr}{dt} \)
\( = 8\pi \dfrac{5}{\sqrt{\pi}}\dfrac{2}{\sqrt{\pi}} \)
\( = 80 \) cm\( ^2 \)/sn
Buna göre kürenin yüzey alanı belirtilen anda 80 cm\( ^2 \)/sn hızla artmaktadır.
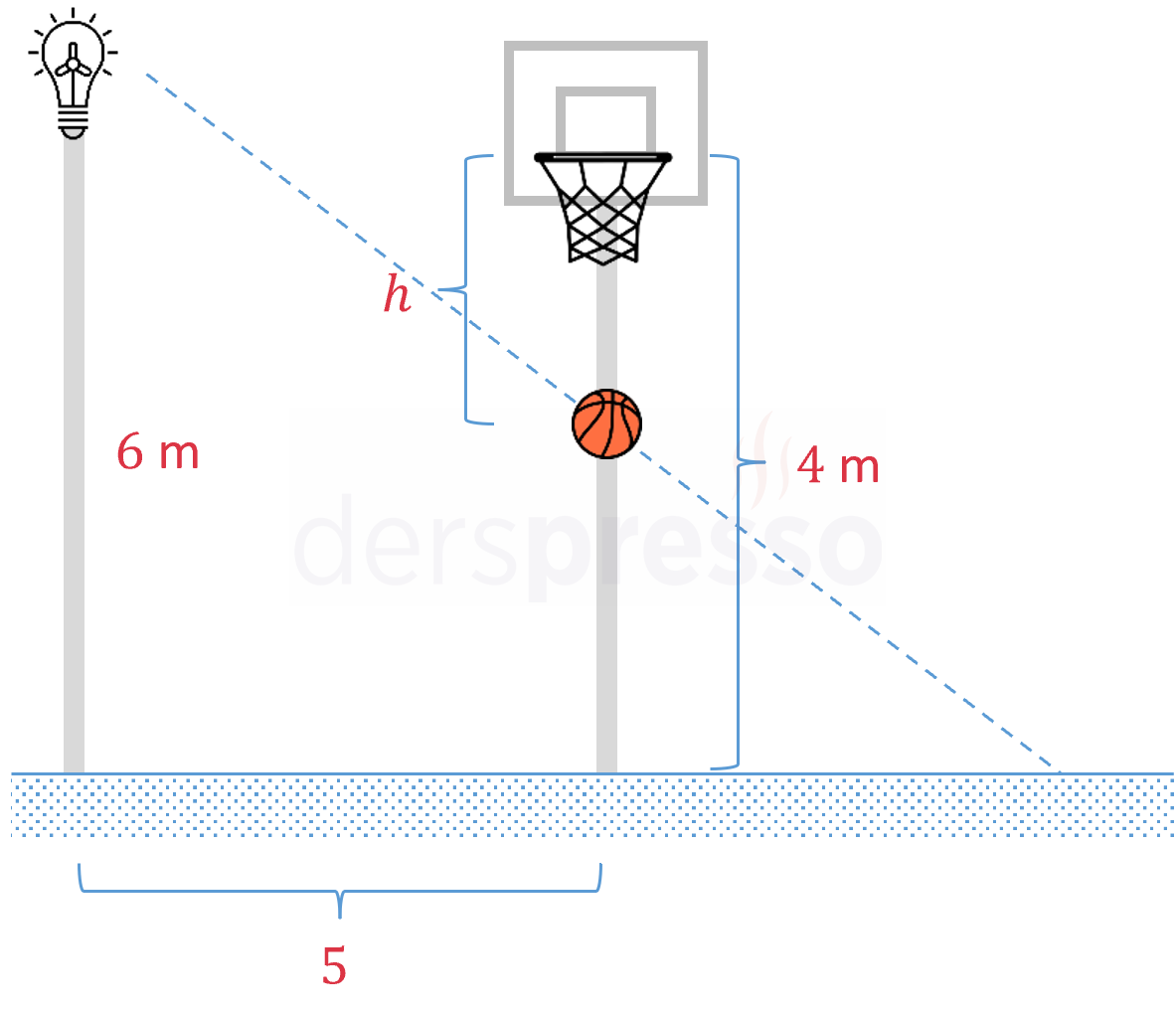
Yerden yüksekliği 6 metre olan bir sokak lambası bir basketbol sahasını aydınlatmaktadır. Sahadaki basketbol potasının yüksekliği 4 metre olup sokak lambasından uzaklığı 5 metredir.
Potaya atılan bir basketbol topunun potadan geçtikten sonraki aşağı yönlü hareketi \( h = 2t^2 \) fonksiyonu ile belirlenmektedir. Buna göre top potadan geçtikten 1 saniye sonra topun yerdeki gölgesinin hareket hızı saniyede kaç metre olur?
Çözümü Göster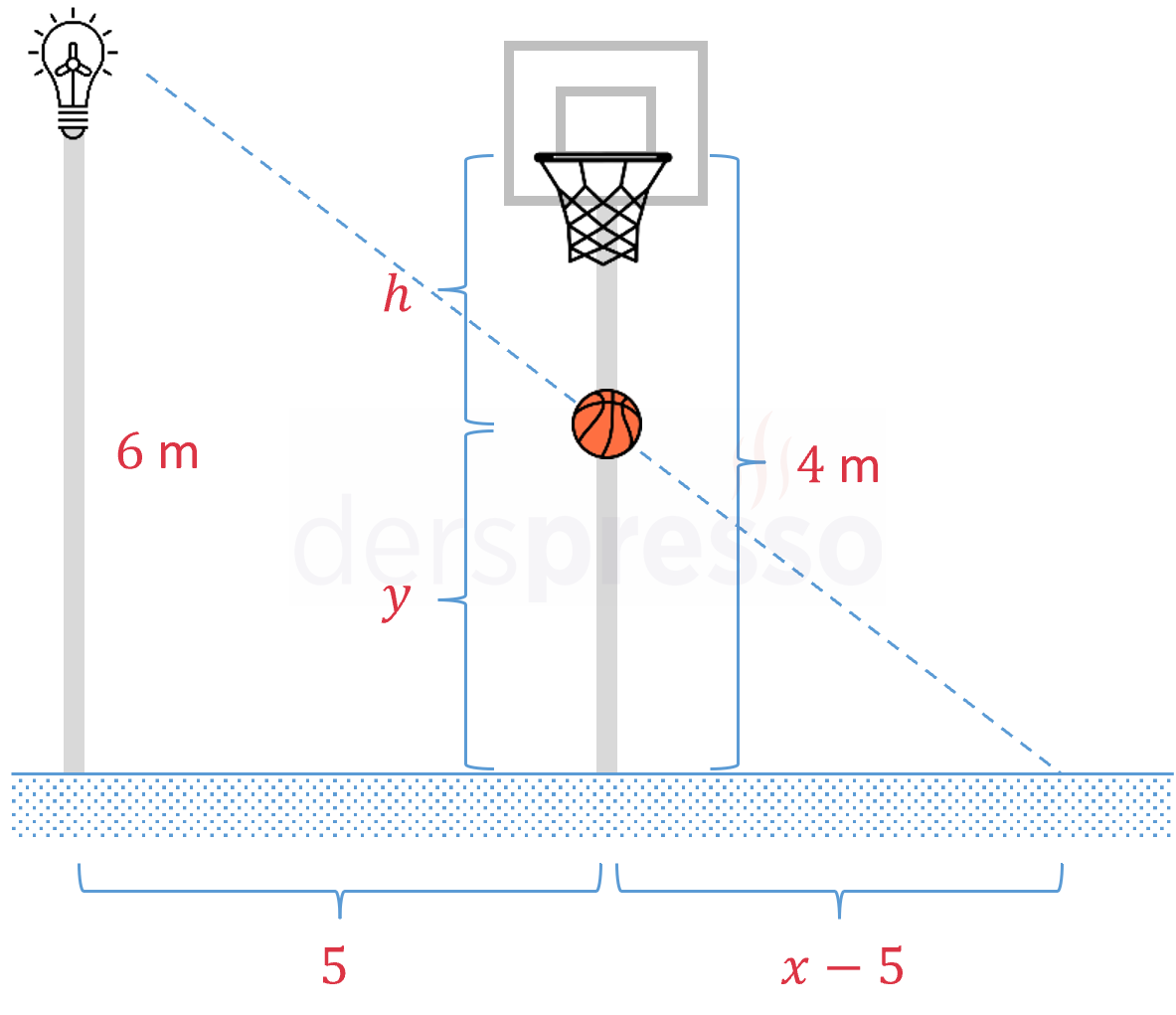
Topun gölgesinin sokak lambasına olan uzaklığına \( x \), topun 1 sn sonra yerden yüksekliğine \( y \) diyelim.
Üçgen benzerliğini kullanalım.
\( \dfrac{y}{6} = \dfrac{x - 5}{x} \)
\( h + y = 4 \)
\( y = 4 - h \)
\( h = 2t^2 \) olarak veriliyor.
\( y = 4 - 2t^2 \)
Bu değeri üçgen benzerliği denkleminde yerine koyalım.
\( \dfrac{4 - 2t^2}{6} = \dfrac{x - 5}{x} \)
İfadeyi düzenleyelim.
\( \dfrac{4}{6} -\dfrac{2t^2}{6} = 1 - \dfrac{5}{x} \)
\( \dfrac{2}{3} -\dfrac{t^2}{3} = 1 - \dfrac{5}{x} \)
\( x \) zamana bağlı değişim gösteren bir değişkendir.
\( \dfrac{2}{3} -\dfrac{t^2}{3} = 1 - \dfrac{5}{x(t)} \)
Eşitliğin iki tarafının zamana göre türevini alalım.
\( -\dfrac{2t}{3} = \dfrac{5}{x^2}\dfrac{dx}{dt} \)
Üçgen benzerliği denklemini kullanarak \( t = 1 \) anındaki \( x \) değerini bulalım.
\( \dfrac{4 - 2(1)^2}{6} = \dfrac{x - 5}{x} \)
\( \dfrac{2}{6} = \dfrac{x - 5}{x} \)
\( x = \dfrac{15}{2} \) m
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( -\dfrac{2(1)}{3} = \dfrac{5}{(\frac{15}{2})^2}\dfrac{dx}{dt} \)
\( \dfrac{dx}{dt} = -\dfrac{15}{2} \) m/sn
Buna göre belirtilen anda topun gölgesi saniyede \( \frac{15}{2} \) metre hızla basket potasına doğru yaklaşmaktadır.
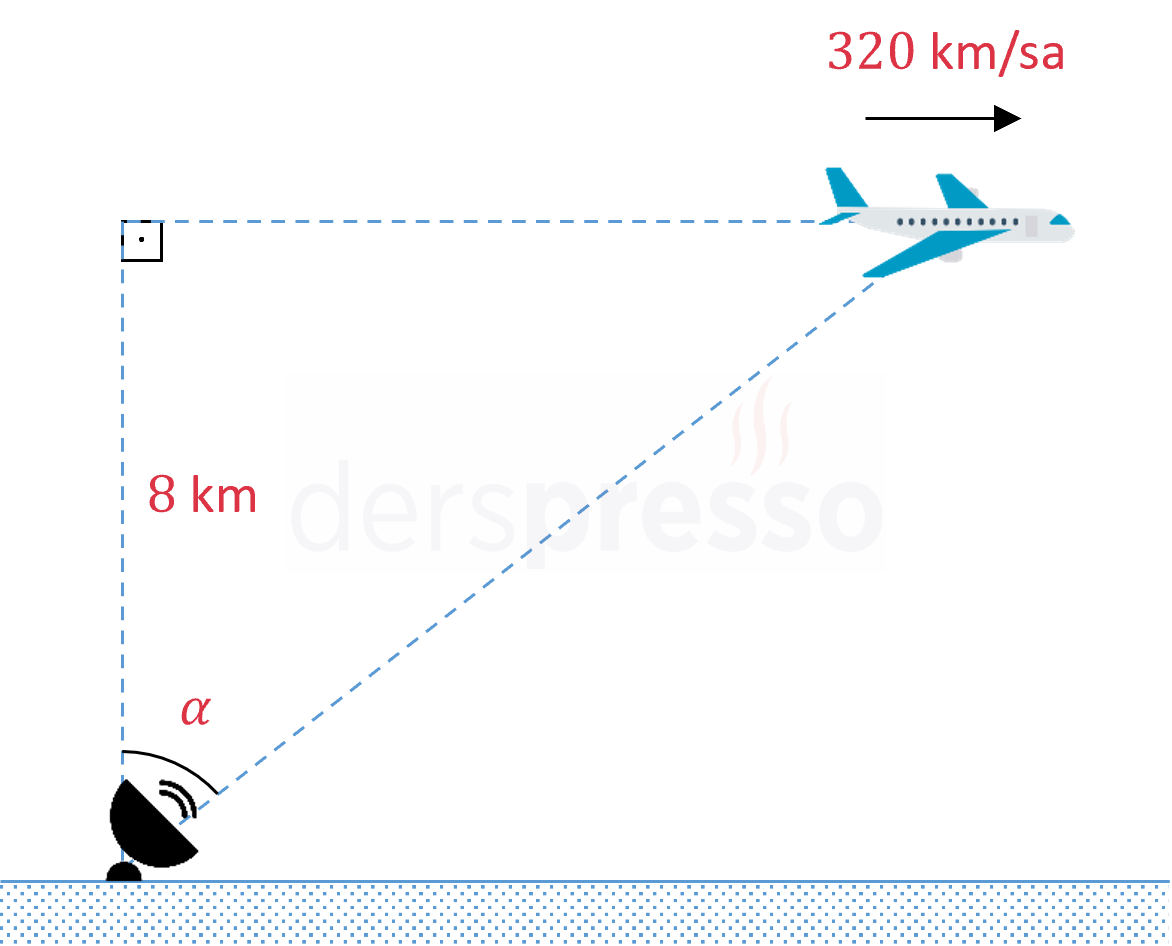
Bir uçak radar istasyonunun 8 km üstünde sabit yükseklikte uçmaktadır. Belirli bir anda şekildeki \( \alpha \) açısı \( \frac{\pi}{6} \) radyandır ve uçak 320 km/sa hızla uçmaktadır. Belirtilen anda \( \alpha \) açısının dakikadaki değişim hızı kaç radyandır?
Çözümü Göster
Uçağın radar istasyonundan yatay uzaklığına \( x \) km diyelim.
\( \tan{\alpha} = \dfrac{x}{8} \)
Uçağın aldığı yol ve \( \alpha \) açısı zamana bağlı değişim gösteren değişkenlerdir.
\( \tan(\alpha(t)) = \dfrac{x(t)}{8} \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \sec^2{\alpha}\dfrac{d\alpha}{dt} = \dfrac{1}{8}\dfrac{dx}{dt} \)
\( \alpha = \frac{\pi}{6} \) radyan olduğu anda \( \alpha \) açısının değişim hızı istenmektedir.
\( \dfrac{d\alpha}{dt} = ? \)
Belirtilen andaki uçağın hızı soruda verilmiştir.
\( \dfrac{dx}{dt} = 320 \) km/sa
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \sec^2{\alpha}\dfrac{d\alpha}{dt} = \dfrac{1}{8}\dfrac{dx}{dt} \)
\( \sec^2{\dfrac{\pi}{6}}\dfrac{d\alpha}{dt} = \dfrac{1}{8}320 \)
\( \sec{\dfrac{\pi}{6}} = \dfrac{2}{\sqrt{3}} \)
\( \dfrac{d\alpha}{dt} = 30 \) radyan/sa
Açının değişim hızını dakika cinsinden yazalım.
\( \dfrac{d\alpha}{dt} = \dfrac{1}{2} \) radyan/dk
Buna göre belirtilen anda \( \alpha \) açısı dakikada \( \frac{1}{2} \) radyan hızla artmaktadır.
Mustafa sakızını nefesiyle saniyede 4 cm\( ^3 \) sabit hızla şişiriyor ve baloncuk yapıyor. Sakız şişirilirken her zaman küresel şekilde kalıyor.
Buna göre aşağıda belirtilen anlarda baloncuğun yarıçapının artış hızı nedir?
(a) Baloncuğun yarıçapı 2 cm olduğu anda
(b) Baloncuğun hacmi \( 36\pi \) cm\( ^3 \) olduğu anda
(c) Sakızı şişirmeye başladıktan 9 saniye sonra
Çözümü GösterKürenin hacim formülünü yazalım.
\( V = \dfrac{4}{3}\pi r^3 \)
Kürenin hacmi ve yarıçapı zamana bağlı değişim gösteren değişkenlerdir.
\( V(t) = \dfrac{4}{3}\pi [r(t)]^3 \)
Bu iki değişkenin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dV}{dt} = 4\pi r^2\dfrac{dr}{dt} \)
Elde ettiğimiz bu denklem baloncuğun hacmi ile yarıçapının zamana bağlı anlık değişim oranları arasındaki ilişkiyi vermektedir.
Soruda baloncuğun yarıçapının belirli anlardaki artış hızı istenmektedir.
\( \dfrac{dr}{dt} = ? \)
Baloncuğun hacminin artış hızı soruda verilmiştir.
\( \dfrac{dV}{dt} = 4 \) cm\( ^3 \)/sn
\( \dfrac{dV}{dt} \) değerini ilişkili oran denkleminde yerine koyalım.
\( 4 = 4\pi r^2\dfrac{dr}{dt} \)
\( \dfrac{dr}{dt} = \dfrac{1}{\pi r^2} \) cm/sn
Elde ettiğimiz bu denklem baloncuğun yarıçapının belirli bir \( r \) değerindeki anlık artış hızını verir.
(a) seçeneği:
Soruda \( r = 2 \) cm anındaki baloncuğun yarıçapının artış hızı istenmektedir.
Bu \( r \) değerini yarıçapın artış hızı denkleminde yerine koyalım.
\( \dfrac{dr}{dt} = \dfrac{1}{\pi r^2} \)
\( = \dfrac{1}{\pi 2^2} = \dfrac{1}{4\pi} \) cm/sn
Buna göre baloncuğun yarıçapı belirtilen anda \( \frac{1}{4\pi} \) cm/sn hızla artmaktadır.
(b) seçeneği:
Soruda \( V = 36\pi \) cm\( ^3 \) anındaki baloncuğun yarıçapının artış hızı istenmektedir.
Kürenin hacim formülünü kullanarak bu \( V \) değerindeki yarıçap değerini bulalım.
\( 36\pi = \dfrac{4}{3}\pi r^3 \)
\( r = 3 \) cm
Bu \( r \) değerini yarıçapın artış hızı denkleminde yerine koyalım.
\( \dfrac{dr}{dt} = \dfrac{1}{\pi r^2} \)
\( = \dfrac{1}{\pi 3^2} = \dfrac{1}{9\pi} \) cm/sn
Buna göre baloncuğun yarıçapı belirtilen anda \( \frac{1}{9\pi} \) cm/sn hızla artmaktadır.
(c) seçeneği:
Soruda sakızı şişirmeye başladıktan 9 saniye sonraki baloncuğun yarıçapının artış hızı istenmektedir.
Baloncuğun hacminin artış hızı soruda verilmiştir.
\( \dfrac{dV}{dt} = 4 \) cm\( ^3 \)/sn
Bu artış hızını kullanarak baloncuğun 9 saniye sonraki hacmini bulalım.
\( V = 9 \cdot 4 = 36 \) cm\( ^3 \)
Kürenin hacim formülünü kullanarak bu \( V \) değerindeki yarıçap değerini bulalım.
\( 36 = \dfrac{4}{3}\pi r^3 \)
\( r = \dfrac{3}{\sqrt[3]{\pi}} \) cm
Bu \( r \) değerini yarıçapın artış hızı denkleminde yerine koyalım.
\( \dfrac{dr}{dt} = \dfrac{1}{\pi r^2} \)
\( = \dfrac{1}{\pi (\dfrac{3}{\sqrt[3]{\pi}})^2} \)
\(= \dfrac{1}{9\sqrt[3]{\pi}} \) cm/sn
Buna göre baloncuğun yarıçapı belirtilen anda \( \frac{1}{9\sqrt[3]{\pi}} \) cm/sn hızla artmaktadır.
Bir zemine 40 cm\( ^3 \)/sn hızla dökülen ince kum, yüksekliği \( h \) cm ve hacmi \( V \) cm\( ^3 \) olan bir yığın meydana getiriyor.
Yığının yüksekliğine bağlı hacim formülü aşağıdaki gibi veriliyor.
\( V = 2h + \sqrt{h^3 + 22} \)
Buna göre yığının yüksekliği 3 cm olduğu anda yüksekliğinin artış hızı kaçtır?
Çözümü GösterYığının hacmi ve yüksekliği zamana bağlı değişkenlerdir.
\( V(t) = 2h(t) + \sqrt{[h(t)]^3 + 22} \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dV}{dt} = 2\dfrac{dh}{dt} + \dfrac{3h^2}{2\sqrt{h^3 + 22}}\dfrac{dh}{dt} \)
\( = \dfrac{dh}{dt}(2 + \dfrac{3h^2}{2\sqrt{h^3 + 22}}) \)
Elde ettiğimiz bu denklem yığının hacmi ve yüksekliğinin zamana bağlı anlık değişim oranları arasındaki ilişkiyi vermektedir.
Soruda \( h = 3 \) cm olduğu andaki yüksekliğin artış hızı istenmektedir.
\( \dfrac{dh}{dt} = ? \)
Yığının hacminin artış hızı soruda verilmiştir.
\( \dfrac{dV}{dt} = 40 \) cm\( ^3 \)/sn
Verilen değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dV}{dt} = \dfrac{dh}{dt}(2 + \dfrac{3h^2}{2\sqrt{h^3 + 22}}) \)
\( 40 = \dfrac{dh}{dt}(2 + \dfrac{3(3)^2}{2\sqrt{3^3 + 22}}) \)
\( 40 = \dfrac{dh}{dt}(2 + \dfrac{27}{14}) \)
\( 40 = \dfrac{dh}{dt}\dfrac{55}{14} \)
\( \dfrac{dh}{dt} = \dfrac{112}{11} \) cm/sn
Buna göre yığının yüksekliği belirtilen anda \( \frac{112}{11} \) cm/sn hızla artmaktadır.

Dik bir duvara yaslanan 10 metre uzunluğundaki merdiven aşağı doğru 25 cm/sn hızla kaymaya başlıyor.
Merdivenin üst kısmının yere olan uzaklığı 6 metre olduğu anda merdivenin duvardan uzaklaşma hızı kaç cm/sn olur?
Çözümü Göster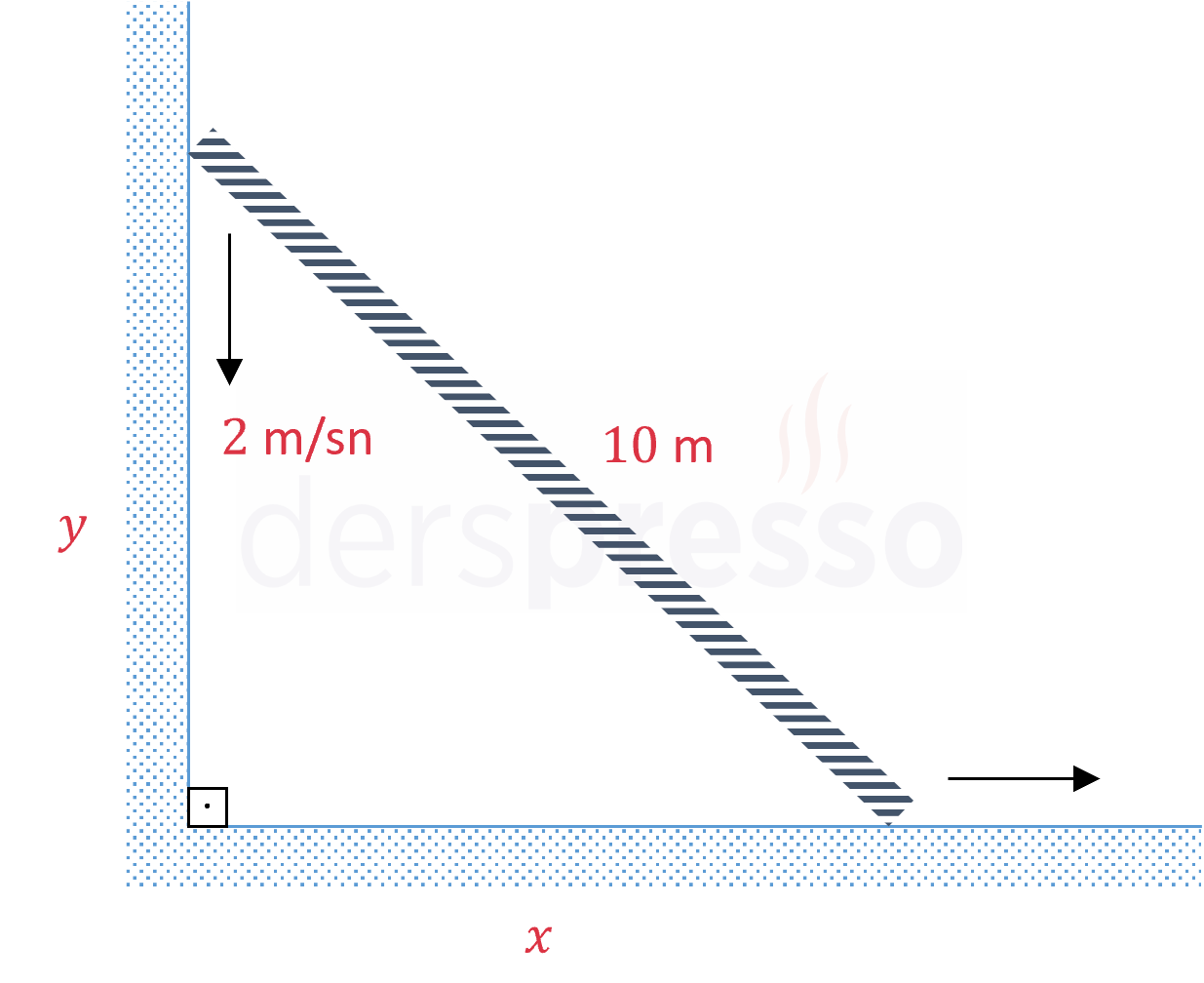
Merdivenin üst kısmının yerden yüksekliğine \( y \), alt kısmının duvardan uzaklığına \( x \) diyelim.
Merdivenin oluşturduğu dik üçgene Pisagor teoremini uygulayalım.
\( 10^2 = y^2 + x^2 \)
Merdivenin üst kısmının yerden yüksekliği ve alt kısmının duvara olan uzaklığı zamana bağlı değişim gösteren değişkenlerdir.
\( 10^2 = [y(t)]^2 + [x(t)]^2 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( 0 = 2y\dfrac{dy}{dt} + 2x\dfrac{dx}{dt} \)
\( 0 = y\dfrac{dy}{dt} + x\dfrac{dx}{dt} \)
Merdivenin duvar boyunca kayma hızı soruda verilmiştir.
\( \dfrac{dy}{dt} = -25 \) cm/sn
\( \dfrac{dy}{dt} = -\dfrac{1}{4} \) m/sn
Merdivenin yere olan uzaklığı \( y = 6 \) metre olduğu andaki duvardan uzaklaşma hızı istenmektedir.
\( \dfrac{dx}{dt} = ? \)
Pisagor teoremini kullanarak \( y = 6 \) olduğu andaki \( x \) değerini bulalım.
\( 10^2 = 6^2 + x^2 \)
\( x = 8 \) m
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( 0 = y\dfrac{dy}{dt} + x\dfrac{dx}{dt} \)
\( 0 = 6(-\dfrac{1}{4}) + 8\dfrac{dx}{dt} \)
\( \dfrac{dx}{dt} = \dfrac{3}{16} \) m/sn
\( \dfrac{dx}{dt} = \dfrac{300}{16} = \dfrac{75}{4} \) cm/sn
Buna göre mediven saniyede \( \frac{75}{4} \) cm hızla duvardan uzaklaşmaktadır.
Tabanı eşkenar olan üçgen prizma şeklinde bir kutunun yüksekliği saniyede 3 cm artarken hacmi saniyede \( \sqrt{3} \) cm\( ^3 \) azalmaktadır.
Buna göre prizmanın taban alanı \( 9\sqrt{3} \) cm\( ^2 \) ve yüksekliği 7 cm olduğu anda tabanın bir kenarının değişim hızı nedir?
Çözümü GösterPrizmanın tabanı eşkenar üçgen olarak verilmiştir.
Prizmanın tabanının bir kenar uzunluğuna \( a \), alanına \( A \), yüksekliğine \( h \) diyelim.
Prizmanın taban alan formülünü \( a \) cinsinden yazalım.
\( A = \dfrac{\sqrt{3}a^2}{4} \)
Prizmanın hacim formülünü yazalım.
\( V = Ah = \dfrac{\sqrt{3}a^2h}{4} \)
Prizmanın hacmi, taban kenar uzunluğu ve yüksekliği zamana bağlı değişim gösteren değişkenlerdir.
\( V(t) = \dfrac{\sqrt{3}[a(t)]^2h(t)}{4} \)
Bu üç değişkenin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( a \) ve \( h \) zamana bağlı değişim gösteren değişkenler oldukları için, çarpımlarının türevini alırken çarpma kuralı kullanılır.
\( \dfrac{dV}{dt} = \dfrac{\sqrt{3}}{4}(2a\dfrac{da}{dt})h + \dfrac{\sqrt{3}}{4}a^2\dfrac{dh}{dt} \)
\( = \dfrac{\sqrt{3}}{2}ah\dfrac{da}{dt} + \dfrac{\sqrt{3}}{4}a^2\dfrac{dh}{dt} \)
Elde ettiğimiz bu denklem prizmanın hacmi, taban kenar uzunluğu ve yüksekliğinin zamana bağlı anlık değişim oranları arasındaki ilişkiyi vermektedir.
Prizmanın hacminin ve yüksekliğinin anlık değişim oranları soruda verilmiştir.
\( \dfrac{dV}{dt} = -\sqrt{3} \) cm\( ^3 \)/sn
\( \dfrac{dh}{dt} = 3 \) cm/sn
Prizmanın anlık taban alanı soruda verilmiştir.
\( A = 9\sqrt{3} \) cm\( ^2 \)
Prizmanın taban alan formülünü kullanarak bu \( A \) değerindeki taban kenar uzunluğunu bulalım.
\( A = \dfrac{\sqrt{3}a^2}{4} \)
\( 9\sqrt{3} = \dfrac{\sqrt{3}a^2}{4} \)
\( a = 6 \) cm
\( A = 9\sqrt{3} \) ve \( h = 7 \) olduğu andaki prizmanın taban kenar uzunluğunun değişim hızı istenmektedir.
\( \dfrac{da}{dt} = ? \)
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dV}{dt} = \dfrac{\sqrt{3}}{2}ah\dfrac{da}{dt} + \dfrac{\sqrt{3}}{4}a^2\dfrac{dh}{dt} \)
\( -\sqrt{3} = \dfrac{\sqrt{3}}{2}(6)(7)\dfrac{da}{dt} + \dfrac{\sqrt{3}}{4}6^2(3) \)
\( -\sqrt{3} = 21\sqrt{3}\dfrac{da}{dt} + 27\sqrt{3} \)
\( \dfrac{da}{dt} = -\dfrac{4}{3} \) cm/sn
Buna göre prizmanın taban kenar uzunluğu belirtilen anda \( \frac{4}{3} \) m/sn hızla azalmaktadır.
Bir kamyon taşıdığı kumu inşaat alanına dökerken taban yarıçapı yüksekliğinin 3 katı olan koni şeklinde bir yığın oluşturuyor.
Kum dakikada 25 m\( ^3 \) hızla döküldüğüne göre, yığının yüksekliği 5 m olduğu andaki yarıçapının artış hızı kaçtır? (Yığın her zaman koni şeklinde kalmaktadır.)
Çözümü GösterKoninin hacim formülünü yazalım.
\( V = \dfrac{1}{3}\pi r^2h \)
Koninin taban yarıçapı yüksekliğinin 3 katı olarak verilmiştir.
\( r = 3h \)
\( h = \dfrac{r}{3} \)
\( h \) değerini koni hacim formülünde yerine yazalım.
\( V = \dfrac{1}{3}\pi r^2(\dfrac{r}{3}) \)
\( = \dfrac{1}{9}\pi r^3 \)
Koninin hacmi ve taban yarıçapı zamana bağlı değişim gösteren değişkenlerdir.
\( V(t) = \dfrac{1}{9}\pi[r(t)]^3 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dV}{dt} = \dfrac{1}{3}\pi r^2\dfrac{dr}{dt} \)
Yığının hacminin artış hızı soruda verilmiştir.
\( \dfrac{dV}{dt} = 25 \) m\( ^3 \)/dk
\( h = 5 \) olduğu andaki yığının yarıçapının artış hızı istenmektedir.
\( \dfrac{dr}{dt} = ? \)
\( h = 5 \) olduğu andaki yığının yarıçapını bulalım.
\( r = 3h \)
\( = 3(5) = 15 \) m
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dV}{dt} = \dfrac{1}{3}\pi r^2\dfrac{dr}{dt} \)
\( 25 = \dfrac{1}{3}\pi(15)^2\dfrac{dr}{dt} \)
\( \dfrac{dr}{dt} = \dfrac{1}{3\pi} \) m/dk
Buna göre yığının yarıçapı belirtilen anda \( \frac{1}{3\pi} \) m/dk hızla artmaktadır.
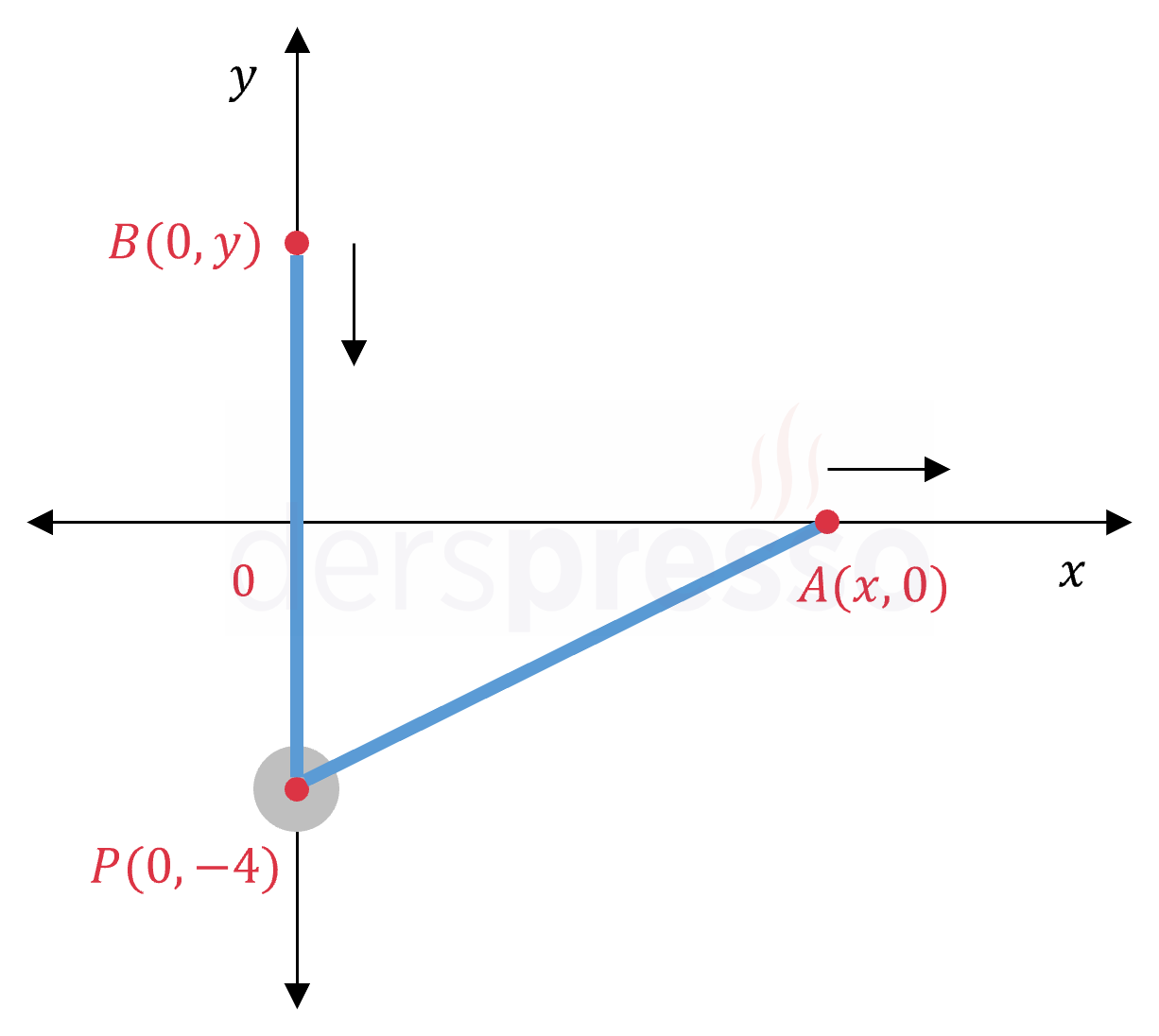
A ve B parçacıkları koordinat düzleminde bulundukları konumlardan ok yönünde hareketlerine başlıyorlar. İki parçacık uzunluğu 20 birim olan, her zaman gergin kalan bir ip ile birbirine bağlıdır ve ip \( P(0, -4) \) noktasında sabit bir makaranın üzerinden geçmektedir.
A parçacığı \( (3, 0) \) noktasında olduğu anda apsis değerindeki değişim hızı 3 birim/sn olduğuna göre, belirtilen anda B parçacığının ordinat değerindeki değişim hızı kaçtır?
Çözümü Göster\( \abs{BP} = y - (-4) = y + 4 \)
Soruda ipin uzunluğu 20 birim olarak veriliyor.
\( \abs{PA} = 20 - (y + 4) \)
\( = 16 - y \)
\( x \) ekseninin altında kalan dik üçgene Pisagor teoremini uygulayalım.
\( \abs{PA}^2 = \abs{OP}^2 + \abs{OA}^2 \)
\( (16 - y)^2 = x^2 + 4^2 \)
A parçacığının \( x \) koordinatı ve B parçacığının \( y \) koordinatı zamana bağlı değişim gösteren değişkenlerdir.
\( (16 - y(t))^2 = [x(t)]^2 + 4^2 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( -2(16 - y)\dfrac{dy}{dt} = 2x\dfrac{dx}{dt} \)
\( \frac{dy}{dt} \) ifadesini yalnız bırakalım.
\( \dfrac{dy}{dt} = -\dfrac{x}{16 - y}\dfrac{dx}{dt} \)
\( x = 3 \) birim olduğu anda B parçacığının ordinat değerindeki değişim hızı istenmektedir.
\( \dfrac{dy}{dt} = ? \)
Pisagor teoremini kullanarak \( x = 3 \) anındaki \( y \) değerini bulalım.
\( (16 - y)^2 = x^2 + 4^2 \)
\( (16 - y)^2 = 3^2 + 4^2 \)
\( y = 11 \) birim
Belirtilen anda A parçacığının apsis değerindeki değişim hızı soruda verilmiştir.
\( \dfrac{dx}{dt} = 3 \) birim/sn
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dy}{dt} = -\dfrac{3}{16 - 11}(3) \)
\( = -1,8 \) birim/sn
Buna göre belirtilen anda B parçacığı saniyede 1,8 birim hızla orijine yaklaşmaktadır.
Bir kürenin hacmi dakikada 24 m\( ^3 \) artmaktadır. Bu kürenin yarıçap uzunluğu 3 m olduğu andaki yüzey alanının artış hızı kaçtır?
Çözümü GösterKürenin yüzey alan formülünü yazalım.
\( A = 4\pi r^2 \)
Kürenin yüzey alanı ve yarıçap uzunluğu zamana bağlı değişim gösteren değişkenlerdir.
\( A(t) = 4\pi [r(t)]^2 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dA}{dt} = 8\pi r\dfrac{dr}{dt} \)
Soruda \( r = 3 \) m olduğu andaki kürenin yüzey alanının artış hızı istenmektedir.
\( \dfrac{dA}{dt} = ? \)
Kürenin hacim formülünü kullanarak \( r = 3 \) olduğu andaki kürenin yarıçapının artış hızını bulalım.
Kürenin hacim formülünü yazalım.
\( V = \dfrac{4}{3}\pi r^3 \)
Kürenin hacmi ve yarıçap uzunluğu zamana bağlı değişim gösteren değişkenlerdir.
\( V(t) = \dfrac{4}{3}\pi [r(t)]^3 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dV}{dt} = 4\pi r^2\dfrac{dr}{dt} \)
Kürenin hacminin artış hızı soruda verilmiştir.
\( \dfrac{dV}{dt} = 24 \) m\( ^3 \)/dk
\( r = 3 \) m olduğu andaki kürenin yarıçapının artış hızını bulalım.
\( \dfrac{dr}{dt} = ? \)
Verilen ve bulduğumuz değerleri hacmin ilişkili oran denkleminde yerine yazalım.
\( \dfrac{dV}{dt} = 4\pi r^2\dfrac{dr}{dt} \)
\( 24 = 4\pi (3^2)\dfrac{dr}{dt} \)
\( \dfrac{dr}{dt} = \dfrac{2}{3\pi} \) m/dk
Verilen ve bulduğumuz değerleri yüzey alanın ilişkili oran denkleminde yerine yazalım.
\( \dfrac{dA}{dt} = 8\pi r\dfrac{dr}{dt} \)
\( = 8 \pi (3)\dfrac{2}{3\pi} \)
\( = 16 \) m\( ^2 \)/dk
Buna göre belirtilen anda kürenin yüzey alanı \( 16 \) m\( ^2 \)/dk hızla artmaktadır.
Alanı 400 cm\( ^2 \) olan bir dikdörtgenin genişliği azalırken yüksekliği saniyede 2 cm sabit hızla artmakta ve alanı sabit kalmaktadır.
(a) Dikdörtgenin genişliği saniyede 0,5 cm hızla azaldığı anda genişliği kaç cm olur?
(b) Dikdörtgenin genişliği 16 cm olduğu anda köşegen uzunluğunun değişim hızı kaç olur?
Çözümü GösterDikdörtgenin genişliğine \( x \), yüksekliğine \( y \) diyelim.
Dikdörtgenin alan formülünü yazalım.
\( A = xy \)
Dikdörtgenin alanı, genişliği ve yüksekliği zamana bağlı değişim gösteren değişkenlerdir.
\( A(t) = x(t)y(t) \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( x \) ve \( y \) zamana bağlı değişim gösteren değişkenler oldukları için, çarpımlarının türevini alırken çarpım kuralı kullanılır.
\( \dfrac{dA}{dt} = \dfrac{dx}{dt}y + x\dfrac{dy}{dt} \)
Dikdörtgenin alanı sabit olduğu için değişim hızı, dolayısıyla türevi 0'dır.
\( 0 = \dfrac{dx}{dt}y + x\dfrac{dy}{dt} \)
Elde ettiğimiz bu denklem dikdörtgenin yüksekliği ile genişliğinin zamana bağlı anlık değişim oranları arasındaki ilişkiyi vermektedir.
(a) seçeneği:
Soruda dikdörtgenin genişliği saniyede 0,5 cm hızla azaldığı andaki dikdörtgenin genişliği istenmektedir.
\( x = ? \)
\( \dfrac{dx}{dt} = -0.5 \) cm/sn
Dikdörtgenin yüksekliğinin artış hızı soruda verilmiştir.
\( \dfrac{dy}{dt} = 2 \) cm/sn
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( 0 = \dfrac{dx}{dt}y + x\dfrac{dy}{dt} \)
\( 0 = -0,5y + x(2) \)
\( 0,5y = 2x \)
\( y = 4x \)
Bulduğumuz \( y \) değerini dikdörtgenin alan formülünde yerine yazalım.
\( A = xy \)
Dikdörtgenin alanı soruda verilmiştir.
\( A = 400 \) cm\( ^2 \)
\( 400 = x(4x) \)
Genişlik negatif değer alamaz.
\( x = 10 \) cm
(b) seçeneği:
Soruda dikdörtgenin genişliği 16 cm olduğu andaki dikdörtgenin köşegen uzunluğunun değişim hızı istenmektedir.
Dikdörtgenin köşegen uzunluğuna \( q \) diyelim.
\( \dfrac{dq}{dt} = ? \)
Dikdörtgenin köşegen uzunluğu Pisagor teoreminden bulunur.
\( q^2 = x^2 + y^2 \)
Dikdörtgenin köşegeni, genişliği ve yüksekliği zamana bağlı değişim gösteren değişkenlerdir.
\( [q(t)]^2 = [x(t)]^2 + [y(t)]^2 \)
Bu üç değişkenin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( 2q\dfrac{dq}{dt} = 2x\dfrac{dx}{dt} + 2y\dfrac{dy}{dt} \)
\( q\dfrac{dq}{dt} = x\dfrac{dx}{dt} + y\dfrac{dy}{dt} \)
Dikdörtgen alan formülünü kullanarak \( x = 16 \) anındaki \( y \) değerini bulalım.
\( 400 = 16y \)
\( y = 25 \) cm
Bulduğumuz \( x, y \) değerlerini köşegen formülünde yerine koyalım.
\( q^2 = x^2 + y^2 \)
\( q^2 = 16^2 + 25^2 \)
\( q = \sqrt{881} \) cm
Dikdörtgenin alanı için ilişkili oran denklemini kullanarak \( x = 16 \) ve \( y = 25 \) olduğu anda dikdörtgenin genişliğinin artış hızını bulalım.
Dikdörtgenin uzunluğunun artış hızı soruda verilmiştir.
\( \dfrac{dy}{dt} = 2 \) cm/sn
\( \dfrac{dA}{dt} = \dfrac{dx}{dt}y + x\dfrac{dy}{dt} \)
\( 0 = \dfrac{dx}{dt}(25) + 16(2) \)
\( \dfrac{dx}{dt} = -\dfrac{32}{25} \)
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine yazalım.
\( q\dfrac{dq}{dt} = x\dfrac{dx}{dt} + y\dfrac{dy}{dt} \)
\( \sqrt{881}\dfrac{dq}{dt} = 16(-\dfrac{32}{25}) + 25(2) \)
\( \dfrac{dq}{dt} = \dfrac{738}{25\sqrt{881}} \) cm/sn
Buna göre belirtilen anda dikdörtgenin köşegen uzunluğu saniyede \( \frac{738}{25\sqrt{881}} \) cm hızla artmaktadır.
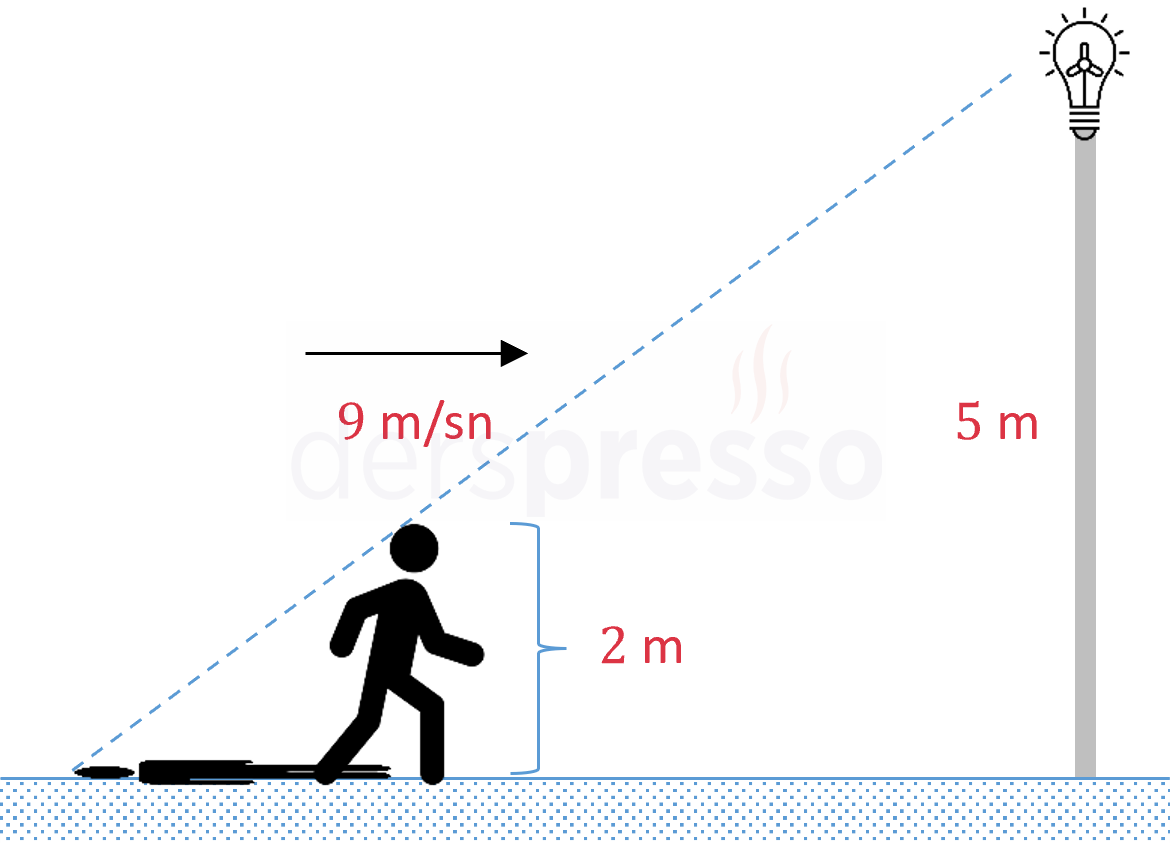
2 metre boyundaki bir adam yerden 5 metre yükseklikte bulunan bir sokak lambasına doğru 9 m/sn hızla yürümektedir. Adamın yerdeki gölgesinin hareket hızı nedir?
Çözümü Göster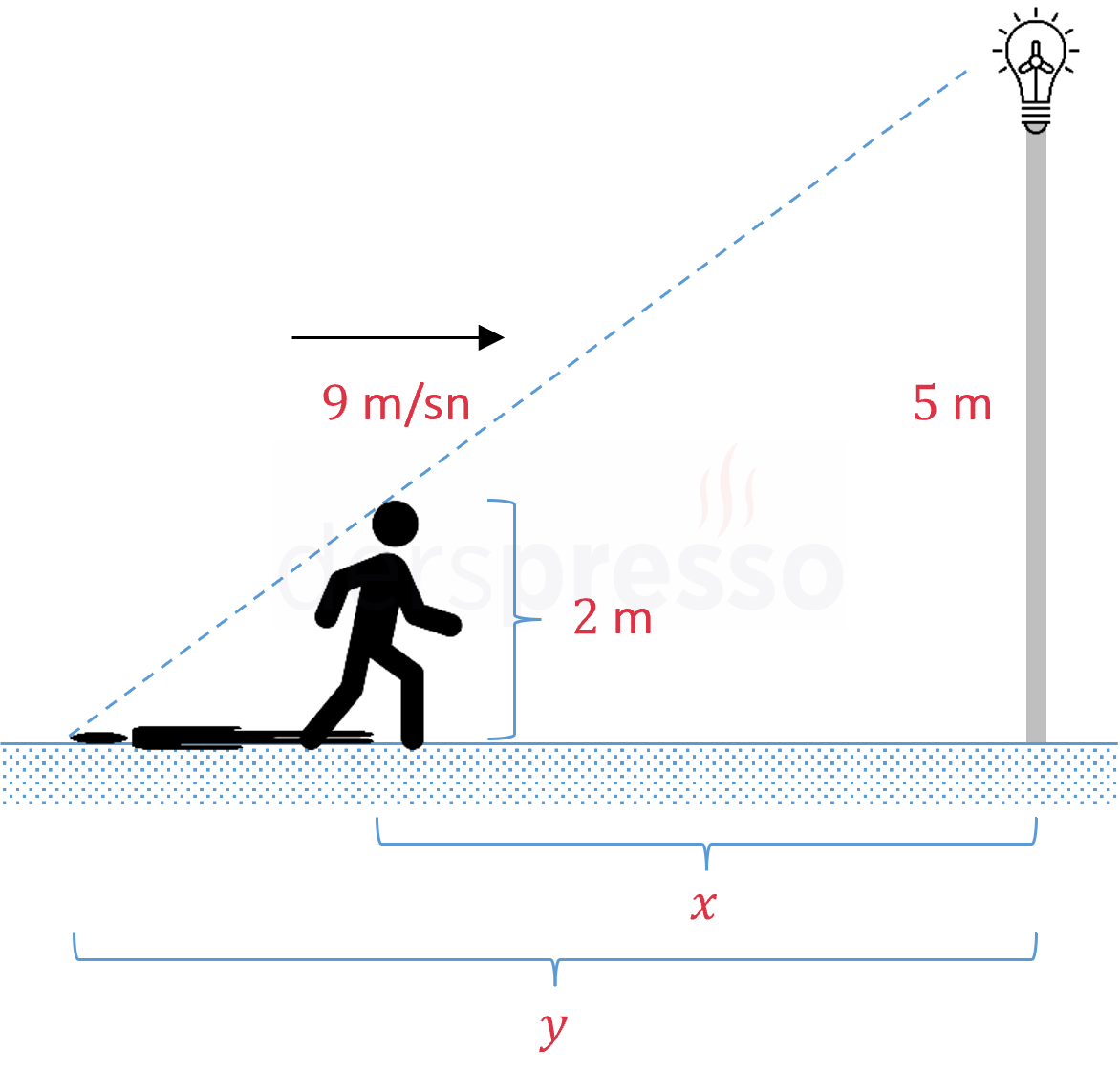
Adamın sokak lambasına olan uzaklığına \( x \), gölgesinin ucunun sokak lambasına olan uzaklığına \( y \) diyelim.
Üçgen benzerliğini kullanalım.
\( \dfrac{2}{5} = \dfrac{y - x}{y} \)
İçler - dışlar çarpımı yapalım.
\( 2y = 5(y - x) \)
\( 3y = 5x \)
\( x \) ve \( y \) değerleri zamana bağlı değişim gösteren değişenlerdir.
\( 3y(t) = 5x(t) \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( 3\dfrac{dy}{dt} = 5\dfrac{dx}{dt} \)
Adamın hızı soruda verilmiştir.
Adam yürüdükçe \( x \) uzaklığı azalmaktadır, dolayısıyla \( x \)'teki değişim hızı negatif olur.
\( \dfrac{dx}{dt} = -9 \) m/sn
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( 3\dfrac{dy}{dt} = 5(-9) \)
\( \dfrac{dy}{dt} = -15 \) m/sn
Buna göre yerdeki adamın gölgesinin ucu saniyede 15 m hızla hareket etmektedir.
Yol kenarında yüksekliği yarıçapının 5 katı uzunlukta olan bir trafik konisi ters çevrilmiş şekilde durmaktadır. Yağan yağmurla birlikte trafik konisine 38 cm\( ^3 \)/sn hızla yağmur suyu dolmaktadır, koninin dibinde bulunan küçük bir delikten ise su sızmaktadır.
Su seviyesinin yüksekliği 15 cm olduğu anda su seviyesinin saniyede \( \frac{4}{\pi} \) cm yükseldiği gözleniyor. Buna göre yağmur suyu trafik konisinden hangi hızda sızmaktadır?
Çözümü GösterTrafik konisinin şekli aşağıdaki gibidir.
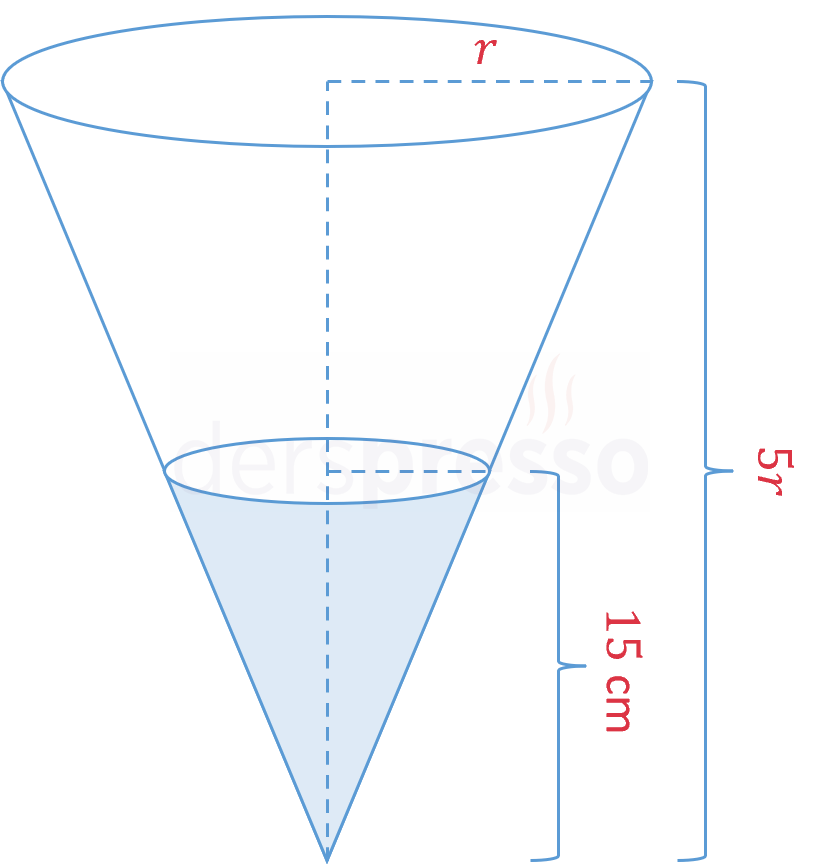
Trafik konisi ve içindeki koni şeklindeki su için hacim formülünü yazalım.
\( V = \dfrac{1}{3}\pi r^2 h \)
Konilerin yüksekliği yarıçapın 5 katı uzunluktadır.
\( h = 5r \)
\( r = \dfrac{h}{5} \)
Bu \( r \) değerini koni hacim formülünde yerine yazalım.
\( V = \dfrac{1}{3}\pi(\dfrac{h}{5})^2h \)
\( = \dfrac{1}{75}\pi h^3 \)
Koninin hacmi ve yüksekliği zamana bağlı değişim gösteren değişkenlerdir.
\( V(t) = \dfrac{1}{75}\pi[h(t)]^3 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dV}{dt} = \dfrac{1}{25}\pi h^2\dfrac{dh}{dt} \)
Su seviyesi \( h = 15 \) cm iken su seviyesinin yükselme hızı soruda verilmiştir.
\( \dfrac{dh}{dt} = \dfrac{4}{\pi} \) cm/sn
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dV}{dt} = \dfrac{1}{25}\pi (15^2)\dfrac{4}{\pi} \)
\( = 36 \) cm\( ^3 \)/sn
Bulduğumuz \( \frac{dV}{dt} = 36 \) cm\( ^3 \)/sn değeri trafik konisi içinde su miktarının artış hızıdır.
Soruda koniye yağmur suyunun dolma hızı 38 cm\( ^3 \)/sn olarak verilmiştir. O halde aradaki fark koniden sızan yağmur suyunun hızıdır.
\( 38 - 36 = 2 \) cm\( ^3 \)/sn
\( x, y, t \) değişkenleri arasındaki ilişki aşağıdaki iki denklemde verilmiştir.
\( y^2 + 2y + 2x - x^3 = 3 \)
\( x^3 = 3t \)
Buna göre \( t = 9 \) anında \( \frac{dy}{dt} \) türevinin alabileceği değerleri bulunuz.
Çözümü GösterZincir kuralını uygulayalım.
\( \dfrac{dy}{dt} = \dfrac{dy}{dx} \cdot \dfrac{dx}{dt} \)
Verilen birinci eşitliğin iki tarafının \( x \)'e göre türevini alalım.
Türevi alırken \( y \) değişkeninin \( x \)'e bağlı bir fonksiyon olduğunu dikkate almalıyız.
\( \dfrac{d(y^2 + 2y + 2x - x^3)}{dx} = \dfrac{d(3)}{dx} \)
\( 2y\dfrac{dy}{dx} + 2\dfrac{dy}{dx} + 2 - 3x^2 = 0 \)
\( \frac{dy}{dx} \) ifadesini yalnız bırakalım.
\( \dfrac{dy}{dx} = \dfrac{3x^2 - 2}{2y + 2} \)
Verilen ikinci eşitliğin iki tarafının \( t \)'ye göre türevini alalım.
Türevi alırken \( x \) değişkeninin \( t \)'ye bağlı bir fonksiyon olduğunu dikkate almalıyız.
\( \dfrac{d(x^3)}{dt} = \dfrac{d(3t)}{dt} \)
\( 3x^2\dfrac{dx}{dt} = 3 \)
\( \frac{dx}{dt} \) ifadesini yalnız bırakalım.
\( \dfrac{dx}{dt} = \dfrac{1}{x^2} \)
Bulduğumuz ifadeleri zincir kuralı formülünde yerine koyalım.
\( \dfrac{dy}{dt} = \dfrac{dy}{dx} \cdot \dfrac{dx}{dt} \)
\( = \dfrac{3x^2 - 2}{2y + 2} \cdot \dfrac{1}{x^2} \)
İkinci eşitliği kullanarak \( t = 9 \) için \( x \) değerini bulalım.
\( x^3 = 3(9) \)
\( x = 3 \)
Birinci eşitliği kullanarak \( x = 3 \) için \( y \) değerini bulalım.
\( y^2 + 2y + 2(3) - 3^3 = 3 \)
\( y^2 + 2y - 24 = 0 \)
\( (y + 6)(y - 4) = 0 \)
\( y = -6 \) ya da \( y = 4 \)
Bu iki \( y \) değeri için ayrı ayrı \( \frac{dy}{dt} \) türevinin değerini bulalım.
\( \dfrac{dy}{dt} = \dfrac{3x^2 - 2}{2y + 2} \cdot \dfrac{1}{x^2} \)
\( \dfrac{dy}{dt}|_{y=-6, x=3} = \dfrac{3(3)^2 - 2}{2(-6) + 2} \cdot \dfrac{1}{3^2} \)
\( = -\dfrac{5}{18} \)
\( \dfrac{dy}{dt}|_{y=4, x=3} = \dfrac{3(3)^2 - 2}{2(4) + 2} \cdot \dfrac{1}{3^2} \)
\( = \dfrac{5}{18} \)
Buna göre \( t = 9 \) için \( \frac{dy}{dt} \) türevi \( \{-\frac{5}{18}, \frac{5}{18} \} \) değerlerini alır.
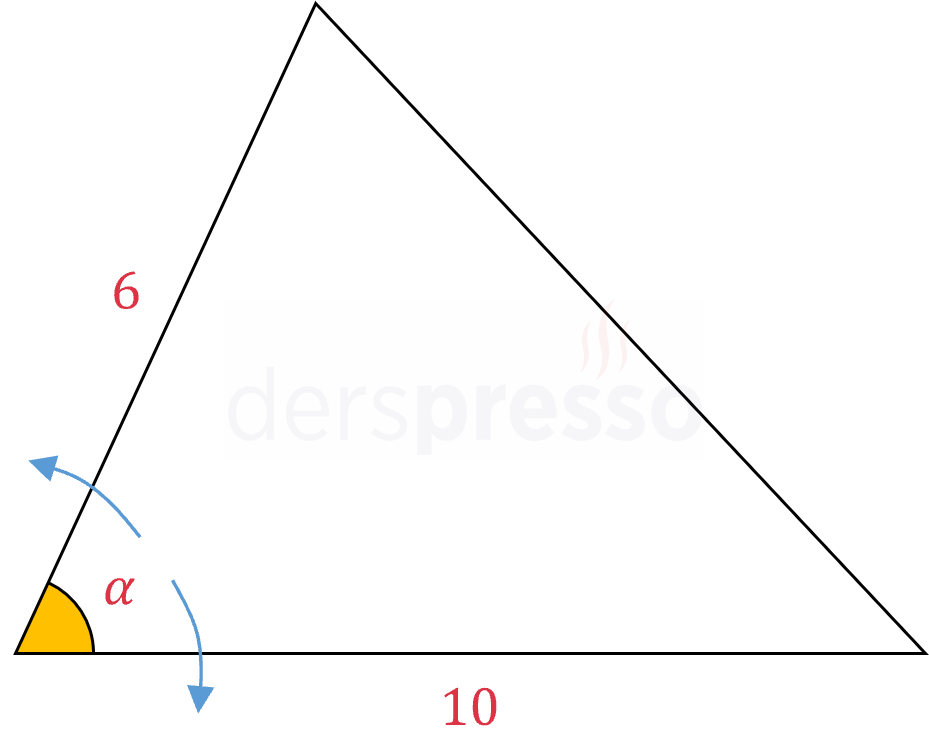
İki kenarının uzunluğu 6 cm ve 10 cm olan bir üçgenin bu iki kenarı arasındaki açı saniyede \( \frac{1}{5} \) radyan hızla artmaktadır.
Üçgenin alanının artış hızı 3 cm\( ^2 \)/sn olduğu anda kenarlar arasındaki açı kaç radyan olur?
Çözümü Göster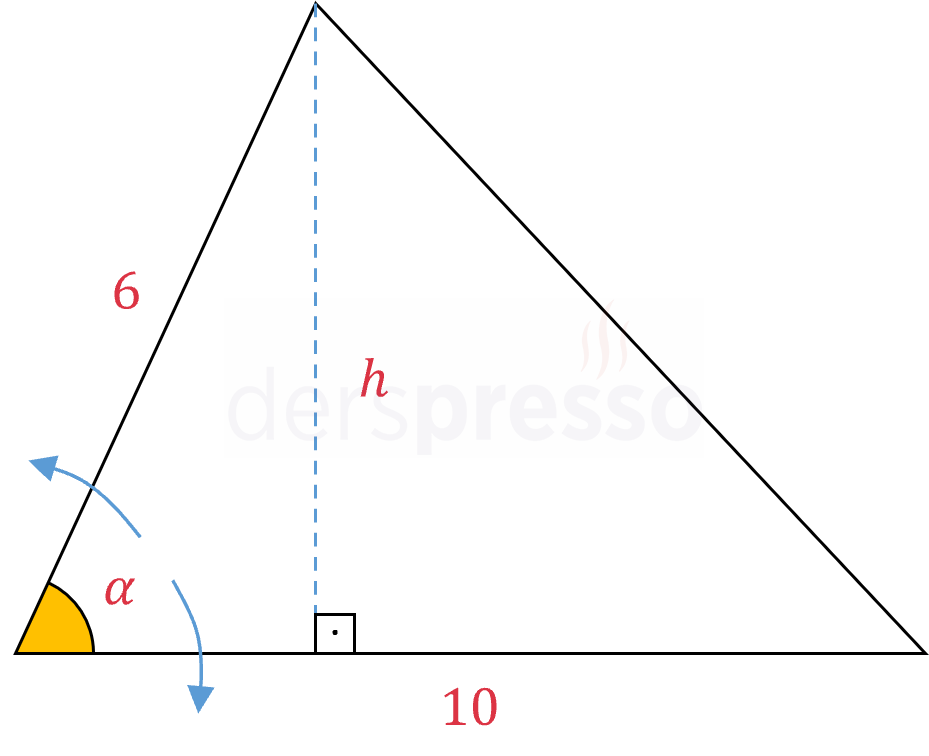
Kenarlar arasındaki açıya \( \alpha \), 10 cm uzunluğundaki tabana ait yüksekliğe \( h \) diyelim.
\( \sin{\alpha} = \dfrac{h}{6} \)
\( h = 6\sin{\alpha} \)
Üçgenin alan formülünü kullanalım.
\( A = \dfrac{10h}{2} = 5h \)
\( h \) değerini formülde yerine koyalım.
\( A = 5(6\sin{\alpha}) = 30\sin{\alpha} \)
Üçgenin alanı ve kenarlar arasındaki açı zamana bağlı değişim gösteren değişkenlerdir.
\( A(t) = 30\sin(\alpha(t)) \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dA}{dt} = 30\cos{\alpha}\dfrac{d\alpha}{dt} \)
Belirtilen anda üçgenin alanının artış hızı soruda verilmiştir.
\( \dfrac{dA}{dt} = 3 \) cm\( ^2 \)/sn
İki kenar arasındaki açının artış hızı soruda verilmiştir.
\( \dfrac{d\alpha}{dt} = \dfrac{1}{5} \) rad/sn
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dA}{dt} = 30\cos{\alpha}\dfrac{d\alpha}{dt} \)
\( 3 = 30\cos{\alpha}\dfrac{1}{5} \)
\( \cos{\alpha} = \dfrac{1}{2} \)
\( \alpha = \dfrac{\pi}{3} \) radyan
Buna göre belirtilen anda bu kenarlar arasındaki açı \( \frac{\pi}{3} \) radyandır.
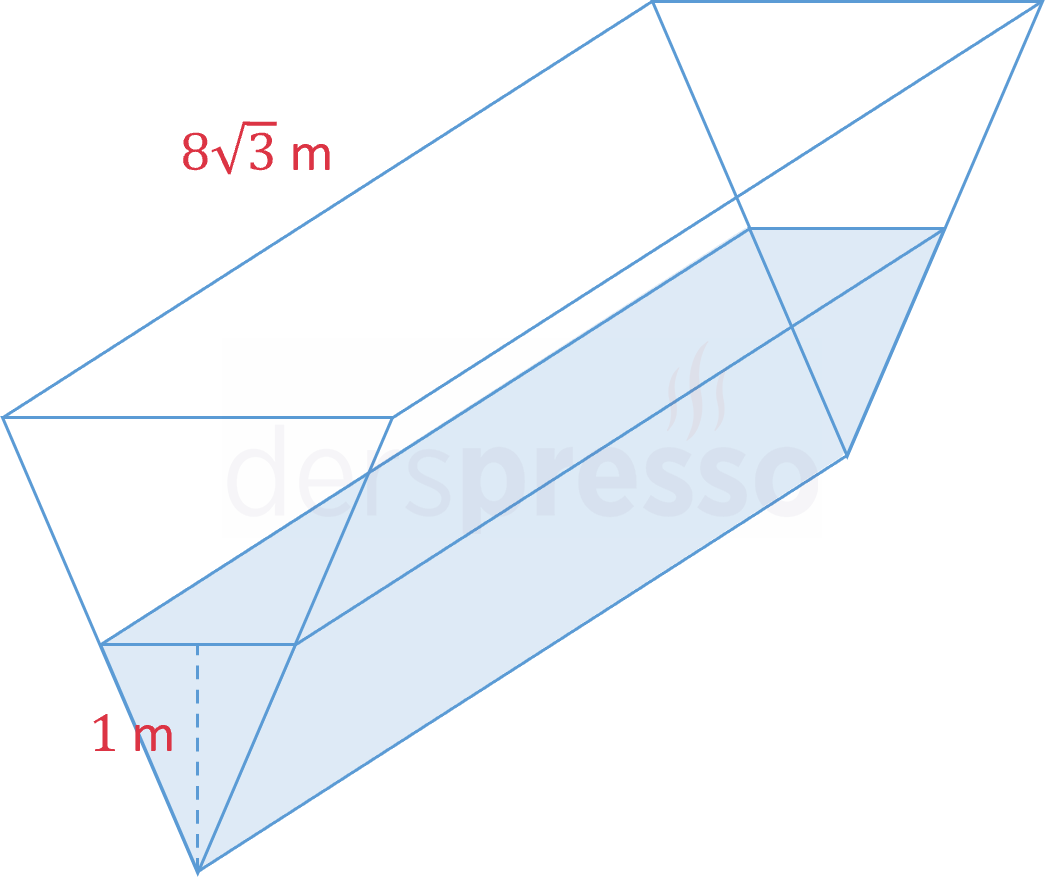
Uzunluğu \( 8\sqrt{3} \) m olan üçgen prizma şeklindeki boş bir havuza su doldurulacaktır. Havuzun yan yüzeyleri eşkenar üçgenlerden oluşmaktadır.
Havuza suyun akış hızı dakikada 18 m\( ^3 \) olduğuna göre, su 1 m yüksekliğe ulaştığında su seviyesinin yükselme hızı kaçtır?
Çözümü GösterHavuzun bir yan yüzey alanına \( A \) diyelim.
Üçgen prizmanın hacim formülünü yazalım.
\( V = 8\sqrt{3}A \)
Prizmanın yan yüzeyi eşkenar üçgen olarak verilmiştir.
Yan yüzeyin bir kenar uzunluğuna \( a \), yüksekliğine \( h \) diyelim.
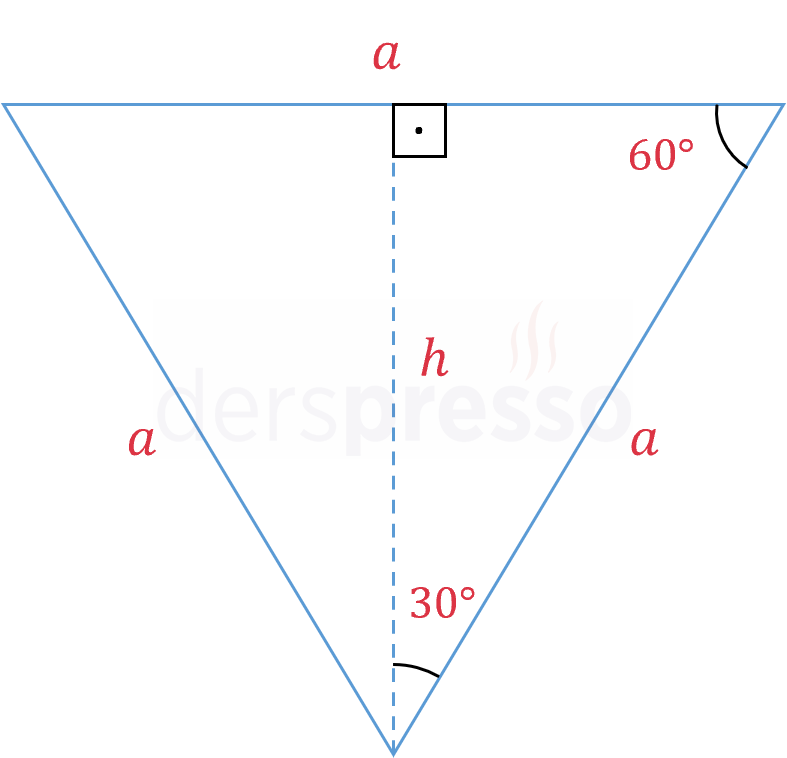
Prizmanın kenar alan formülünü yazalım.
\( A = \dfrac{ah}{2} \)
\( \cos{30°} = \dfrac{h}{a} = \dfrac{\sqrt{3}}{2} \)
\( a = \dfrac{2h}{\sqrt{3}} \)
Bu değeri prizmanın kenar alan formülünde yerine koyalım.
\( A = \dfrac{\frac{2h}{\sqrt{3}}h}{2} \)
\( = \dfrac{h^2}{\sqrt{3}} \)
Bu değeri prizmanın hacim formülünde yerine koyalım.
\( V = 8\sqrt{3}A \)
\( = 8\sqrt{3}\dfrac{h^2}{\sqrt{3}} \)
\( = 8h^2 \)
Üçgen prizmanın hacmi ve yüksekliği zamana bağlı değişim gösteren değişkenlerdir.
\( V(t) = 8[h(t)]^2 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dV}{dt} = 16h\dfrac{dh}{dt} \)
Suyun akış hızı soruda verilmiştir.
\( \dfrac{dV}{dt} = 18 \) m\( ^3 \)/dk
\( h = 1 \) m olduğu andaki havuzun yüksekliğinin artış hızı istenmektedir.
\( \dfrac{dh}{dt} = ? \)
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine yazalım.
\( \dfrac{dV}{dt} = 16h\dfrac{dh}{dt} \)
\( 18 = 16(1)\dfrac{dh}{dt} \)
\( \dfrac{dh}{dt} = \dfrac{9}{8} \) m/dk
Buna göre belirtilen anda su seviyesinin yüksekliği \( \frac{9}{8} \) m/sdk hızla artmaktadır.
Esra öğretmen fizik dersinde öğrencilerine genleşme konusunu anlatırken deney yapmak için sınıfa taban yarıçapı \( r \) cm ve yüksekliği \( 5r \) cm olan koni şeklinde bir metal getirmiştir ve koni ısıtılınca koninin genleştiği gözlenmiştir.
Koninin taban alanının artış hızı 0,24 cm\( ^2 \)/sn olduğuna göre, koninin taban yarıçapı 3 cm olduğu andaki hacminin artış hızı kaçtır?
Çözümü GösterSoruda önce taban alanının artış hızını kullanarak yarıçapın anlık değişim hızını bulalım, daha sonra bu değeri hacmin anlık artış hızını bulmak için kullanalım.
Koninin taban alan formülünü yazalım.
\( A = \pi r^2 \)
Koni tabanının alanı ve yarıçapı zamana bağlı değişim gösteren değişkenlerdir.
\( A(t) = \pi[r(t)]^2 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
Türevi alırken \( r \) değişkeninin \( t \)'ye bağlı bir fonksiyon olduğunu dikkate almalıyız.
\( \dfrac{dA}{dt} = 2\pi r\dfrac{dr}{dt} \)
Elde ettiğimiz bu denklem koni tabanının alanı ile yarıçapının zamana bağlı anlık değişim oranları arasındaki ilişkiyi vermektedir.
Koninin taban alanının artış hızı soruda verilmiştir.
\( \dfrac{dA}{dt} = 0,24 \) cm\( ^2 \)/sn
\( r = 3 \) olduğu andaki yarıçapın artış hızını bulalım.
\( \dfrac{dr}{dt} = ? \)
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dA}{dt} = 2\pi r\dfrac{dr}{dt} \)
\( 0,24 = 2\pi (3)\dfrac{dr}{dt} \)
\( \dfrac{dr}{dt} = \dfrac{1}{25\pi} \) cm/sn
Koni hacim formülünü yazalım.
\( V = \dfrac{1}{3}\pi r^2h \)
Koninin yüksekliği soruda \( h = 5r \) olarak verilmiştir.
\( V = \dfrac{1}{3}\pi r^2(5r) \)
\( = \dfrac{5}{3}\pi r^3 \)
Koninin hacmi ve yarıçapı zamana bağlı değişim gösteren değişkenlerdir.
\( V(t) = \dfrac{5}{3}\pi[r(t)]^3 \)
Bu değişkenlerin zamana bağlı değişim oranları arasındaki ilişkiyi bulmak için eşitliğin iki tarafının zamana göre türevini alalım.
\( \dfrac{dV}{dt} = 5\pi r^2\dfrac{dr}{dt} \)
Elde ettiğimiz bu denklem koninin hacmi ile yarıçapının zamana bağlı anlık değişim oranları arasındaki ilişkiyi vermektedir.
Soruda \( r = 3 \) cm olduğu andaki koninin hacminin artış hızı istenmektedir.
\( \dfrac{dV}{dt} = ? \)
Verilen ve bulduğumuz değerleri ilişkili oran denkleminde yerine koyalım.
\( \dfrac{dV}{dt} = 5\pi r^2\dfrac{dr}{dt} \)
\( = 5\pi (3)^2\dfrac{1}{25\pi} \)
\( = \dfrac{9}{5} \) cm\( ^3 \)/sn
Buna göre koninin hacmi belirtilen anda \( \frac{9}{5} \) cm\( ^3 \)/sn hızla artmaktadır.