Teğet Problemi
Önceki bölümde gördüğümüz üzere; bir fonksiyonun belirli bir noktadaki anlık değişim oranı fonksiyona o noktada çizilen teğet doğrunun eğimine eşittir, dolayısıyla bir noktadaki anlık değişim oranı için bu noktadaki teğet doğrunun eğimini bulmamız gerekmektedir.
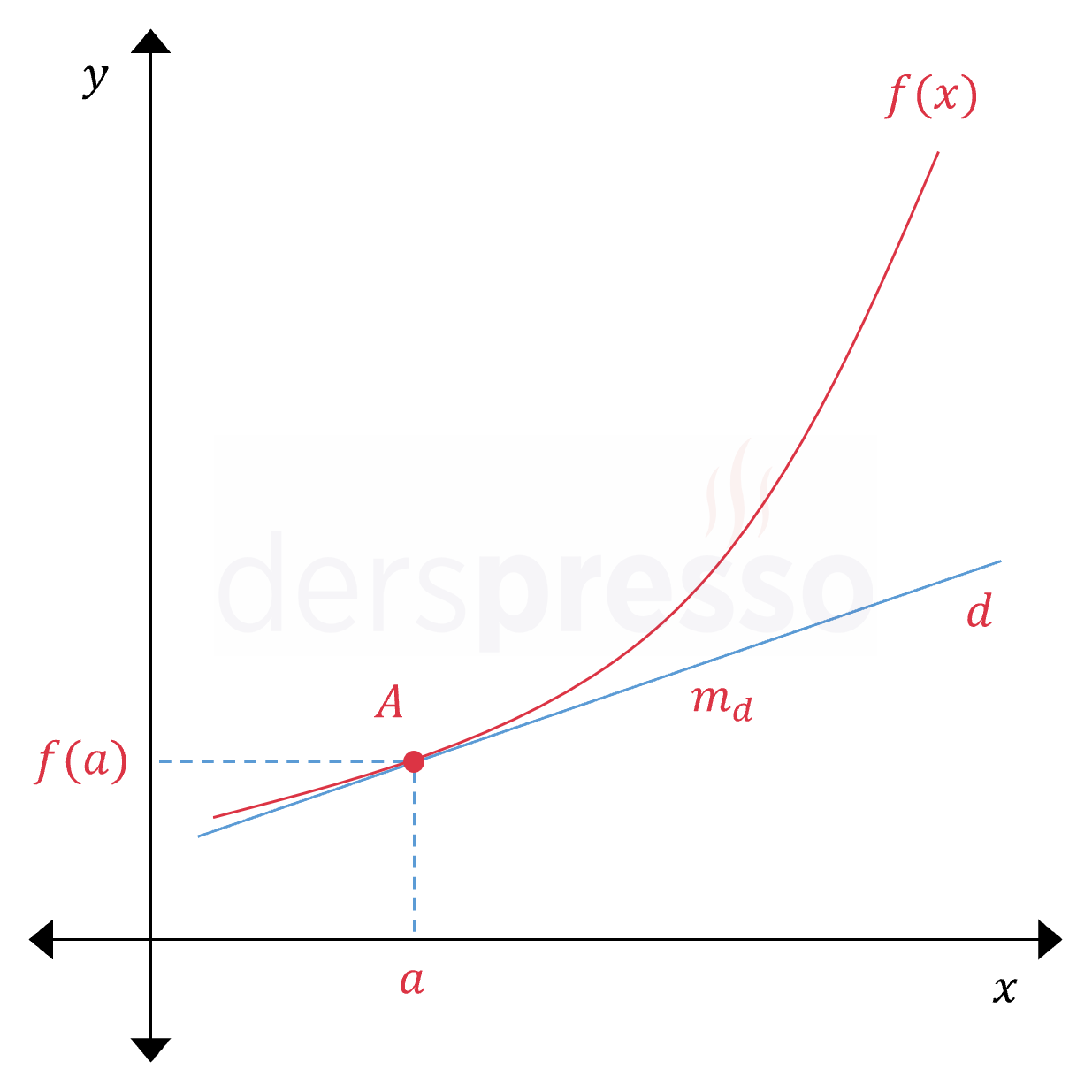
\( A \) noktasındaki anlık değişim oranı \( = m_d \)
Doğrunun eğimi formülünü kullanabilmek için doğrunun geçtiği iki noktanın bilinmesi gerekir. \( d \) doğrusu için sadece \( A \) noktası bilindiği için farklı bir yönteme ihtiyaç duyulacaktır.
\( A \) noktası dışında ikinci bir nokta olarak eğri üzerinde herhangi bir \( B_1 \) noktası seçtiğimizi ve \( [AB_1] \) kesen doğrusunun eğimini hesapladığımızı varsayalım. \( B_1 \) noktasını \( A \) noktasının uzağında seçersek bulacağımız eğim değeri \( d \) doğrusunun eğiminden oldukça farklı olacaktır. Bu ikinci noktayı sırayla \( B_2 \), \( B_3 \) ve \( B_4 \) noktaları olarak gitgide \( A \) noktasına yakın seçtiğimizde, elde edeceğimiz eğim değeri de \( d \) doğrusunun eğimine gitgide yaklaşacaktır.
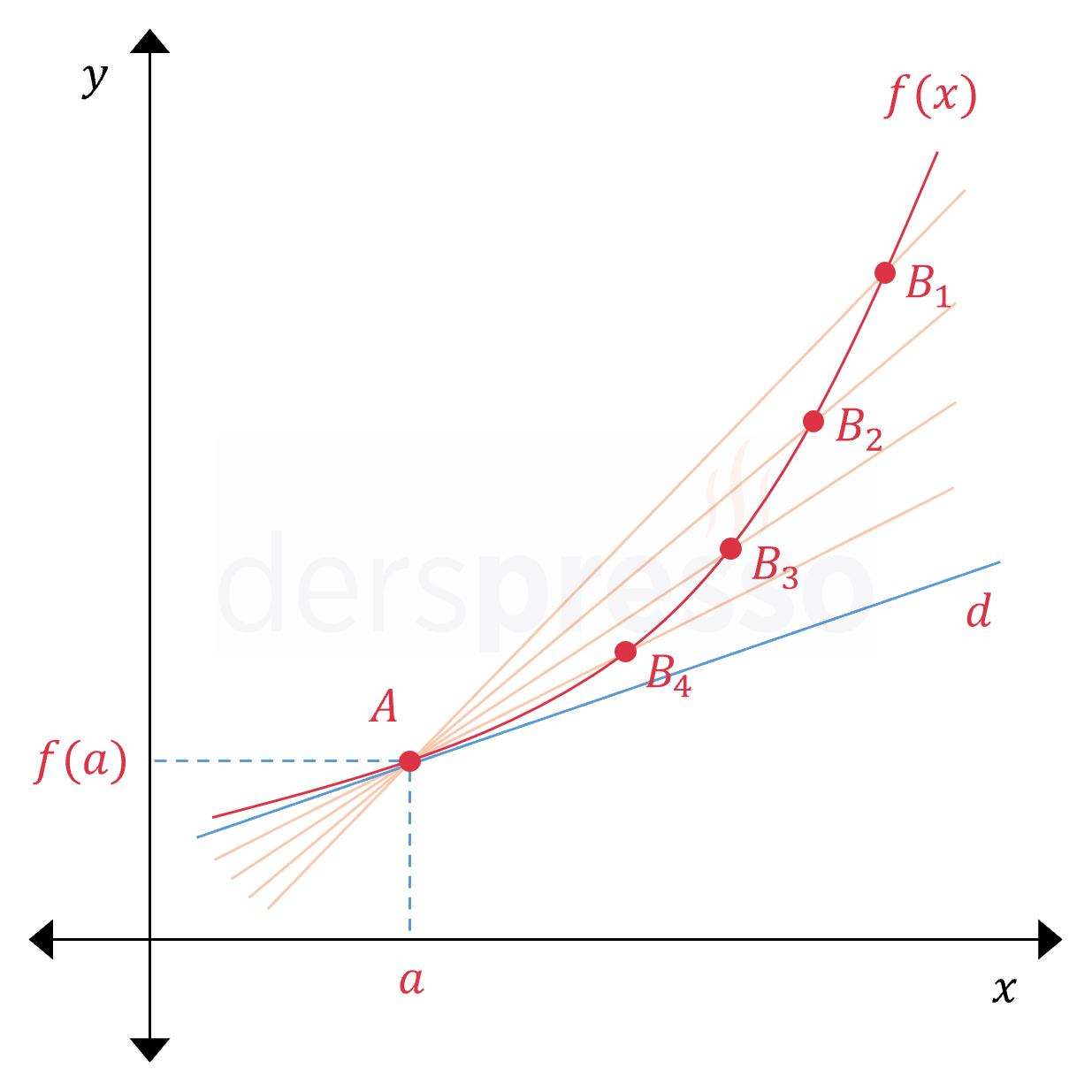
Dolayısıyla \( d \) doğrusunun eğimine en yakın değeri bulabilmek için, ikinci \( B \) noktasını \( A \) noktasına gitgide yaklaştırarak kesen doğrunun eğimini hesaplamamız gerekir. "Gitgide yaklaşan" noktalardan bahsettiğimiz için de bu eğim denklemini bir limit ifadesi şeklinde yazabiliriz.
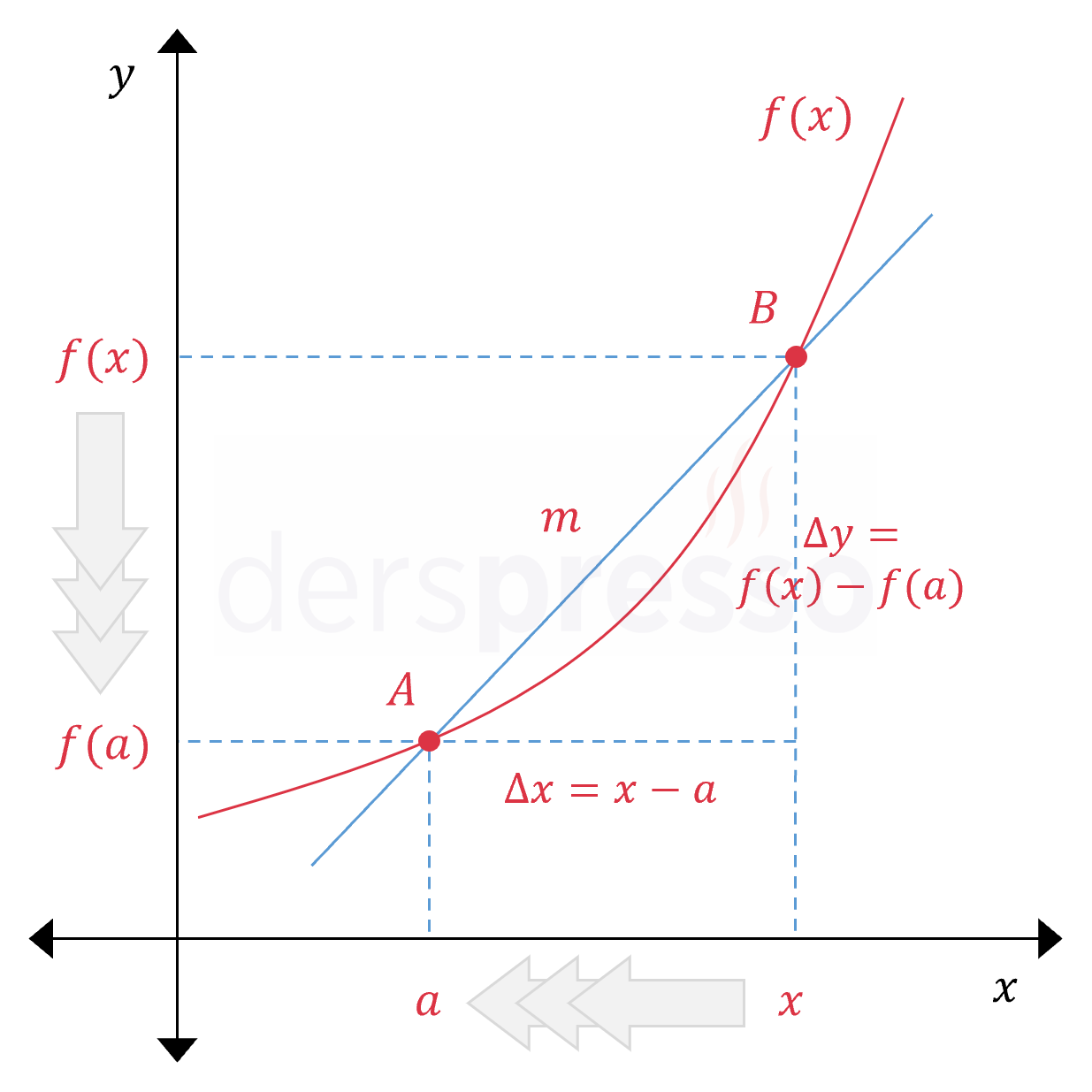
\( \text{Anlık değişim oranı} = m \) \( = \lim\limits_{x \to a} {\dfrac{f(x) - f(a)}{ x - a}} \)
Yukarıdaki limit ifadesi \( x \) değeri \( a \)'ya yaklaşırken \( [AB] \) kesen doğrusunun eğimini verir ve bu değer \( x \) \( a \)'ya sınırsız yaklaştığında \( d \) doğrusunun eğimine, dolayısıyla \( A \) noktasındaki anlık değişim oranına eşit olur.
Bir hareketlinin zamana (saat) bağlı konumunu (km) veren fonksiyon aşağıdaki gibidir.
\( f(t) = 4t^2 \)
Bu hareketlinin \( t = 2 \) anındaki hızı saatte kaç km'dir?
Konum - zaman fonksiyonunun belirli bir noktadaki eğimi o noktadaki anlık hızı verir.
Hareketlinin \( t = 2 \) anındaki hızını, anlık değişim oranının limit tanımını kullanarak hesaplayalım.
\( \lim\limits_{t \to 2} \dfrac{f(t) - f(2)}{t - 2} \)
\( = \lim\limits_{t \to 2} \dfrac{4t^2 - 4(2)^2}{t - 2} \)
\( = \lim\limits_{t \to 2} \dfrac{4(t^2 - 4)}{t - 2} \)
\( t = 2 \) koyduğumuzdaki hem pay hem de payda sıfır olur, dolayısıyla limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
\( \frac{0}{0} \) belirsizliğini pay ve paydadaki ortak \( t - 2 \) çarpanını sadeleştirerek giderelim.
\( = \lim\limits_{t \to 2} \dfrac{4(t - 2)(t + 2)}{t - 2} \)
\( = \lim\limits_{t \to 2} 4(t + 2) \)
Limiti alınan ifade doğrusal bir fonksiyon ve tüm reel sayılarda sürekli olduğu için doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( = 4(2 + 2) = 16 \) km/s bulunur.
Anlık değişim oranı tüm noktalarda 0 olan bir \( f \) fonksiyonunun \( x = 5 \) noktasındaki değerinin 10 olduğu biliniyor.
Buna göre \( f(22) - f(8) \) kaçtır?
Çözümü GösterAnlık değişim oranı tüm noktalarda 0 ise \( f \) bir sabit fonksiyondur.
\( f(5) = 10 \) ise fonksiyon tüm noktalarda bu sabit değere eşittir.
\( f(x) = 10 \)
\( f(22) - f(8) = 10 - 10 = 0 \) bulunur.