Değişim Oranı

Delta sembolü ($$) matematikte (diğer anlamları yanında) bir değişkenin değerindeki değişimi ifade eder.

Değişim oranı ya da bir diğer ifadeyle değişim hızı ise bir değişkendeki değişimin diğer bir değişkendeki değişime oranıdır. İki farklı değişim oranından bahsedebiliriz.

• Ortalama değişim oranı
• Anlık değişim oranı

Bu iki değişim oranını incelemeden önce, bir fonksiyon grafiği üzerinde çizilebilecek iki farklı doğru tipini kısaca tanımlamamız faydalı olacaktır.

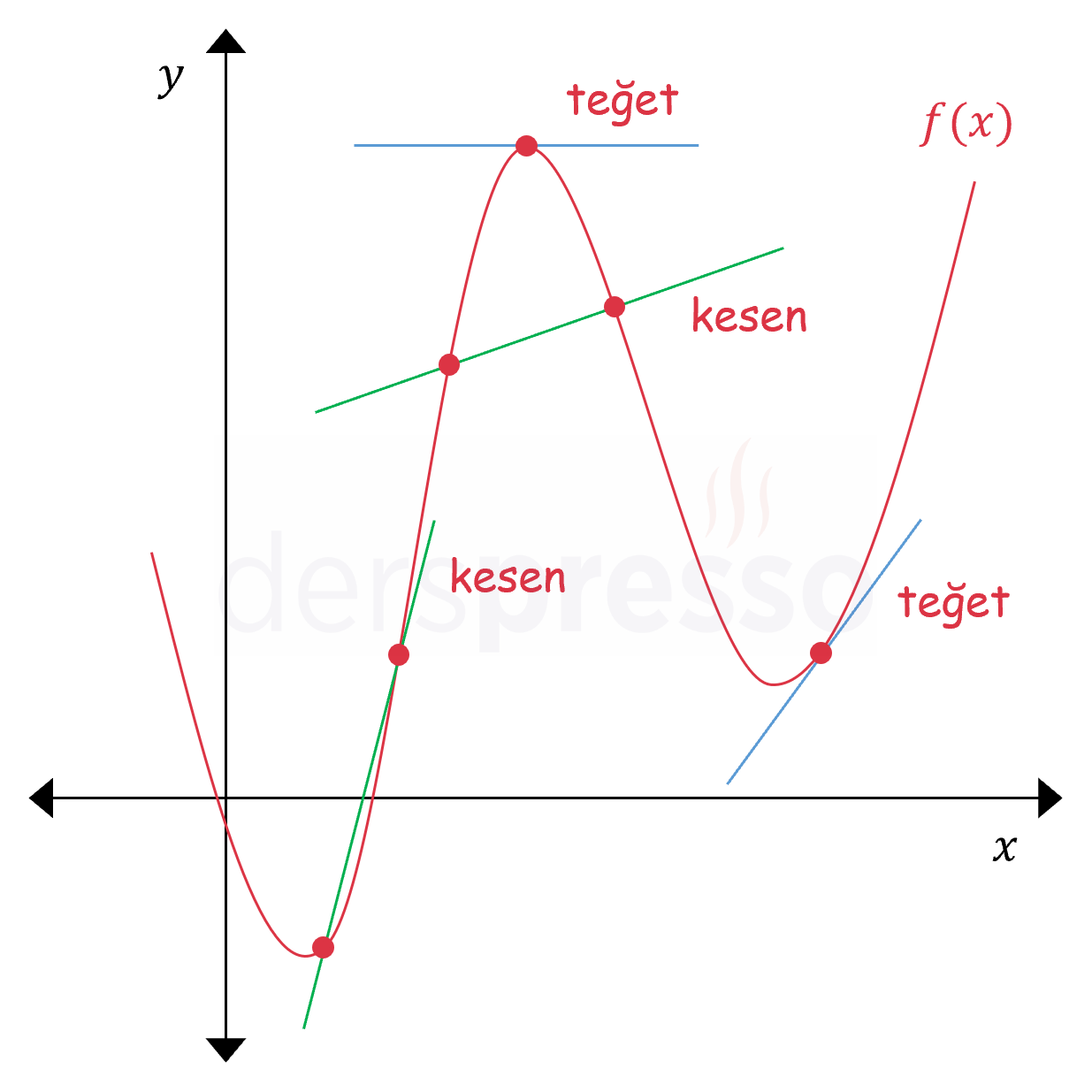
Bir fonksiyon grafiğini iki (ya da daha fazla) noktada kesen doğruya kesen doğru denir. Bir fonksiyon grafiğini belirli bir nokta civarında bir kez kesen ve fonksiyonun bu nokta civarındaki davranışını en doğru şekilde temsil eden doğruya ise teğet doğru denir. Bu tanım teğet doğrunun en doğru tanımı olmayıp gerçek tanımı türeve dayanmaktadır.

Aşağıdaki şekilde bir fonksiyon grafiğine çizilen iki teğet ve iki kesen doğru gösterilmiştir.

Ortalama Değişim Oranı

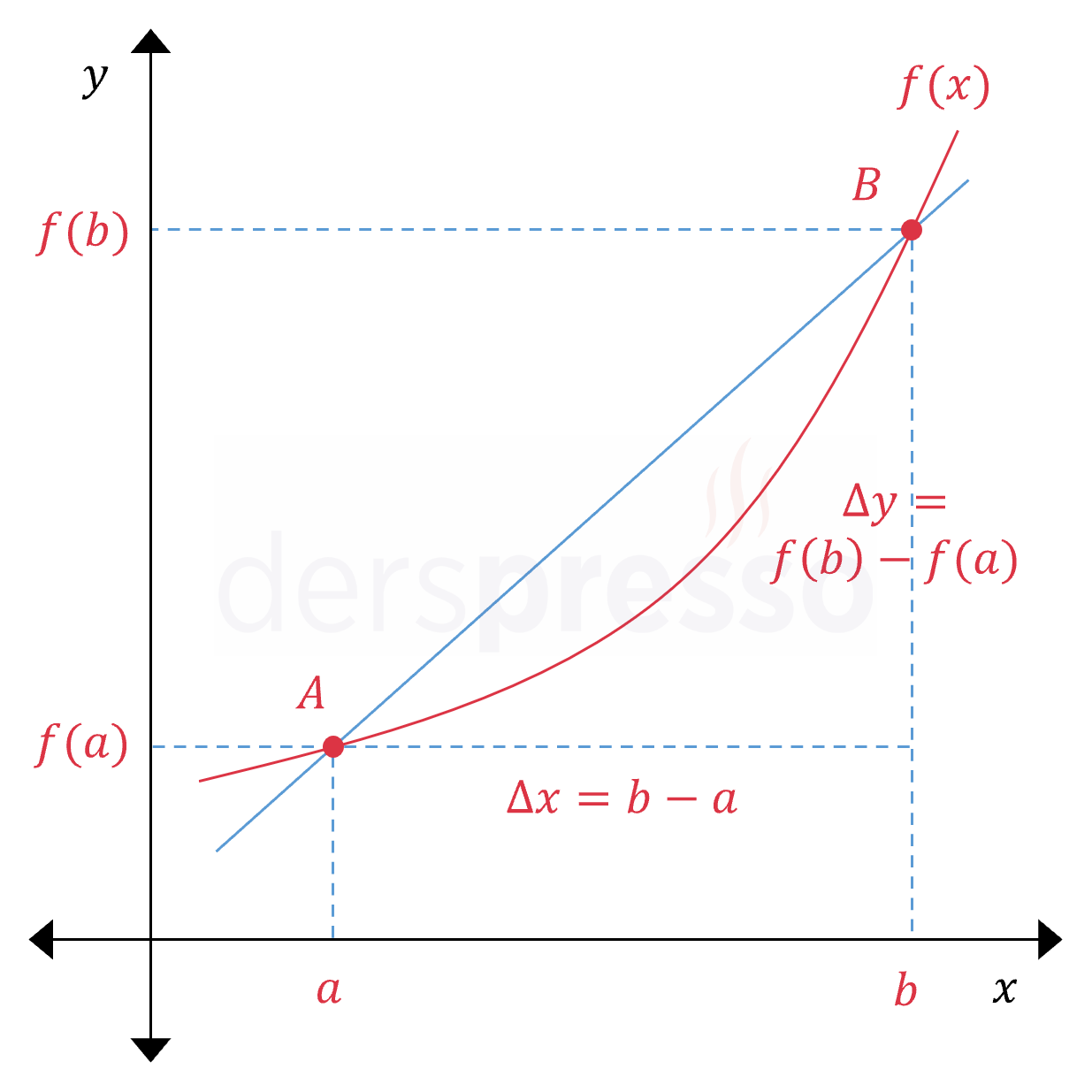
Bir fonksiyonun iki farklı noktası arasındaki ortalama değişim oranı, fonksiyonun bu iki nokta arasında çıktı değişkenindeki değişimin ($$) girdi değişkenindeki değişime ($$) oranıdır. Ortalama değişim oranı aynı zamanda bu iki noktayı birleştiren kesen doğrunun eğimine eşittir.

Doğrusal fonksiyonlarda ortalama değişim oranı tüm doğru boyunca sabittir ve doğrunun eğimine eşittir.

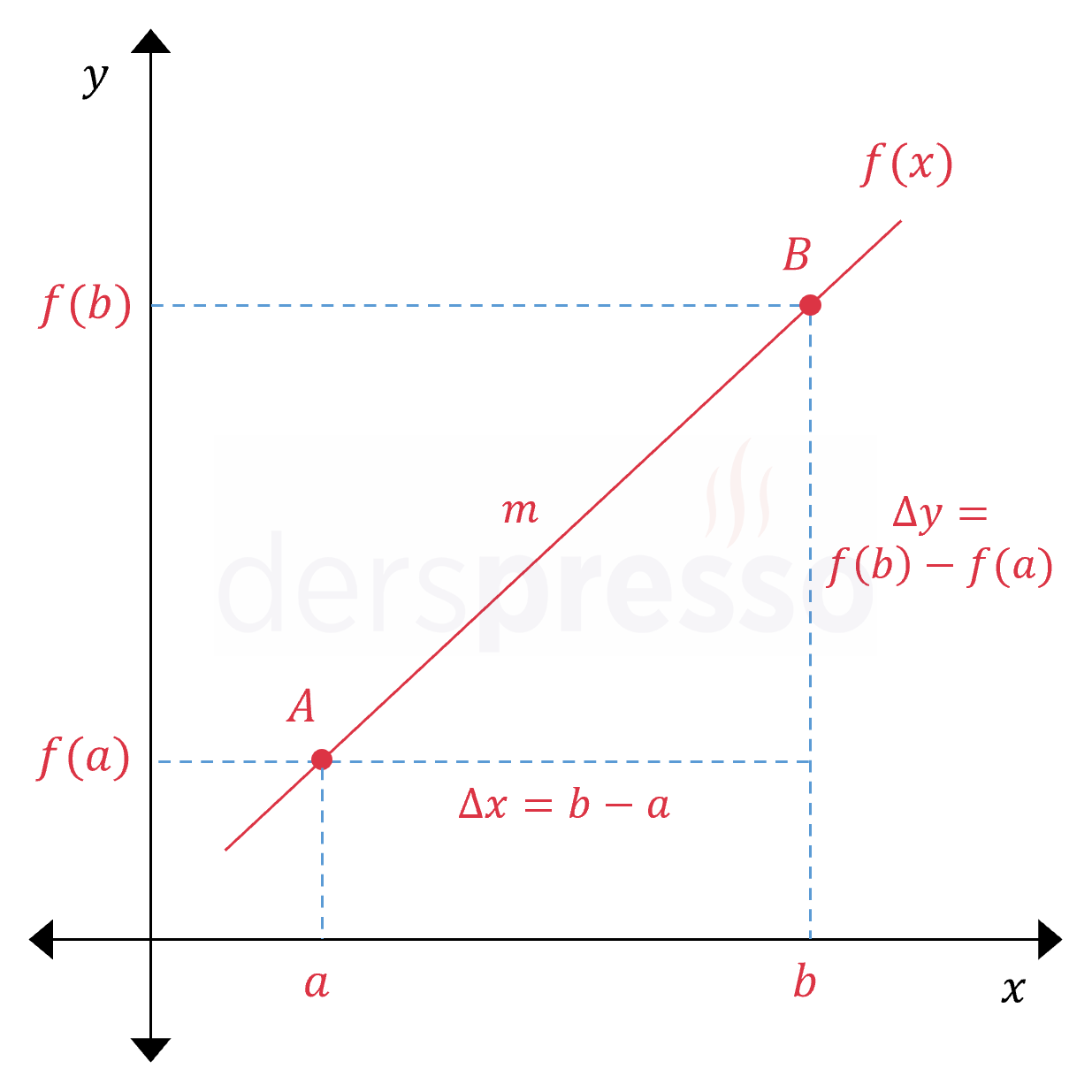
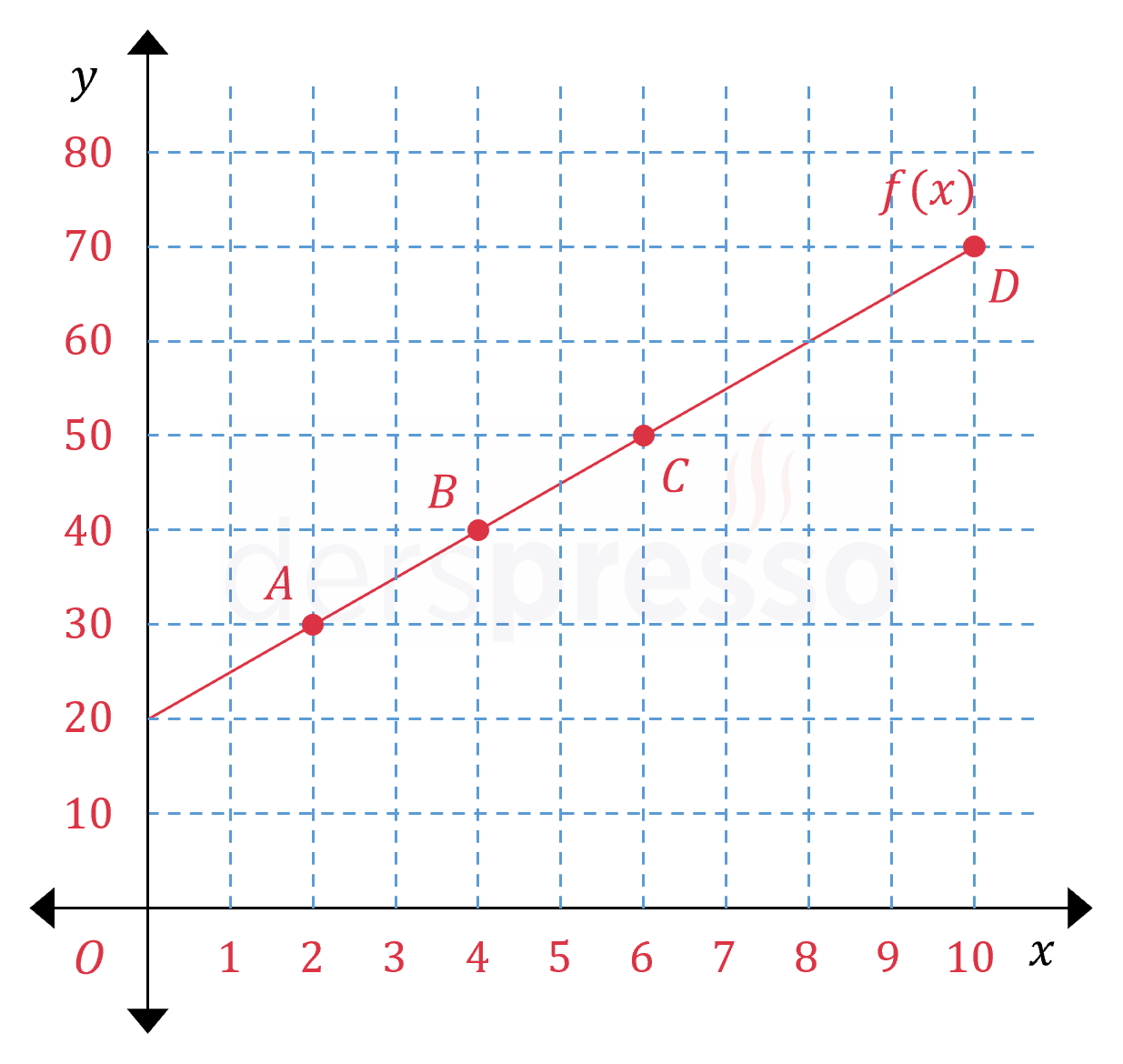
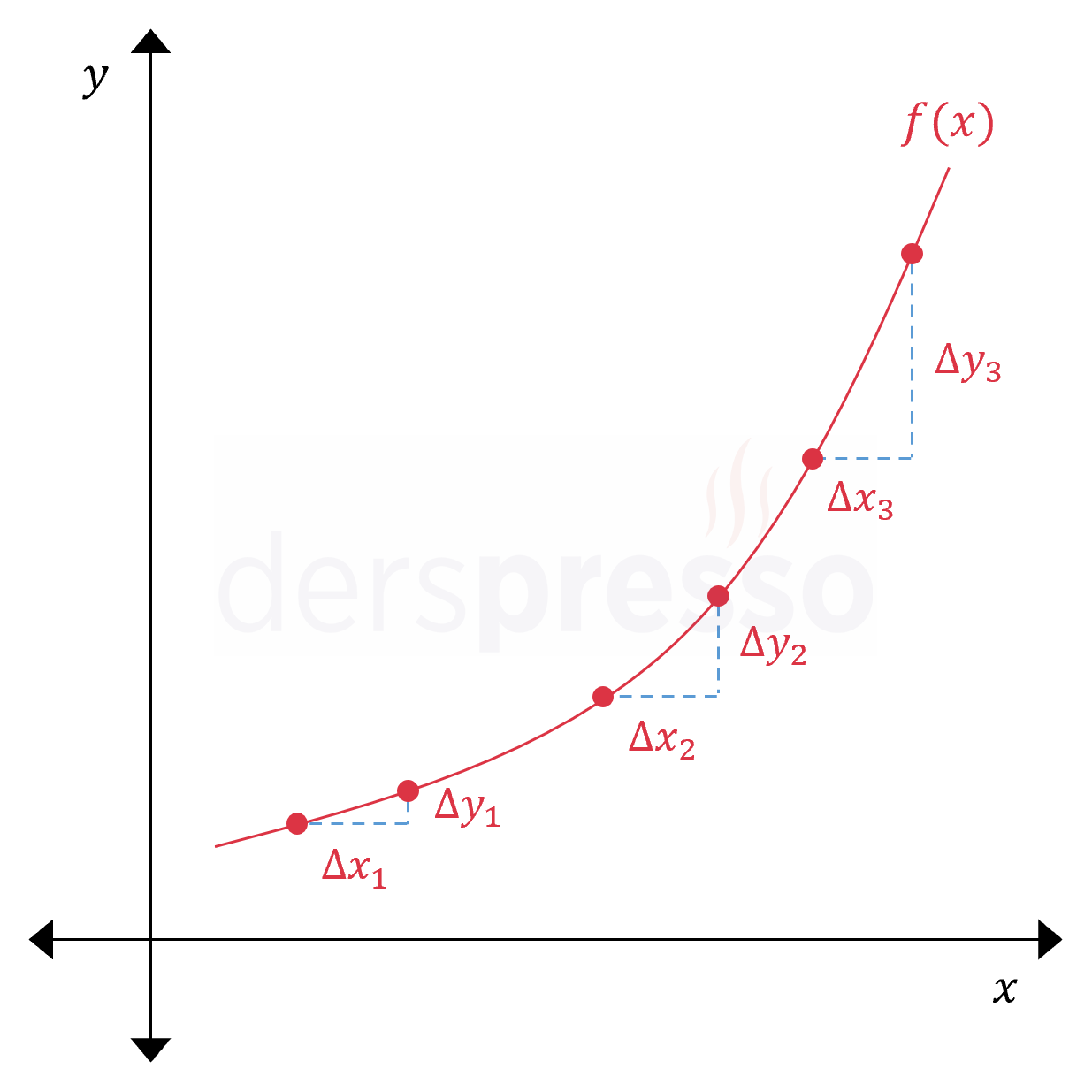
Doğrusal olmayan fonksiyonlarda ise ortalama değişim oranı fonksiyonun farklı aralıklarında farklı değerlere sahip olabilir. Örneğin aşağıda grafiği verilen fonksiyon üç farklı aralıkta üç farklı değişim oranına sahiptir (grafikte sağa doğru ilerledikçe $$'teki aynı birim değişim için $$'deki değişim artmaktadır).

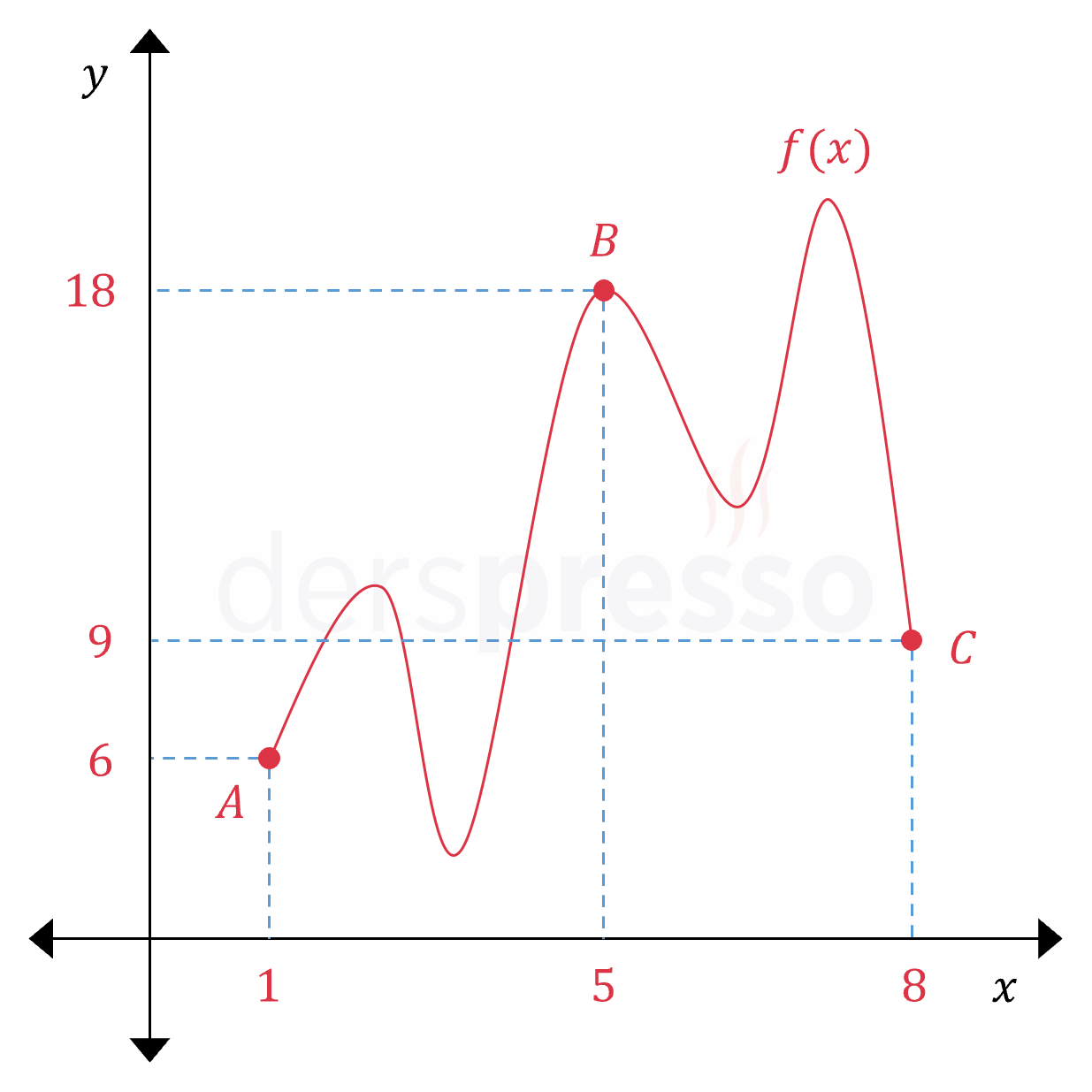
İki nokta arasındaki ortalama değişim oranı sadece bu iki noktanın ordinat ve apsis değerlerine bağlıdır, fonksiyonun iki nokta arasındaki davranışını dikkate almaz. Örneğin aşağıdaki grafikteki dört fonksiyon $$ aralığında çok farklı davranışlar gösterse de, bu aralıktaki ortalama değişim oranları birbirine eşittir.

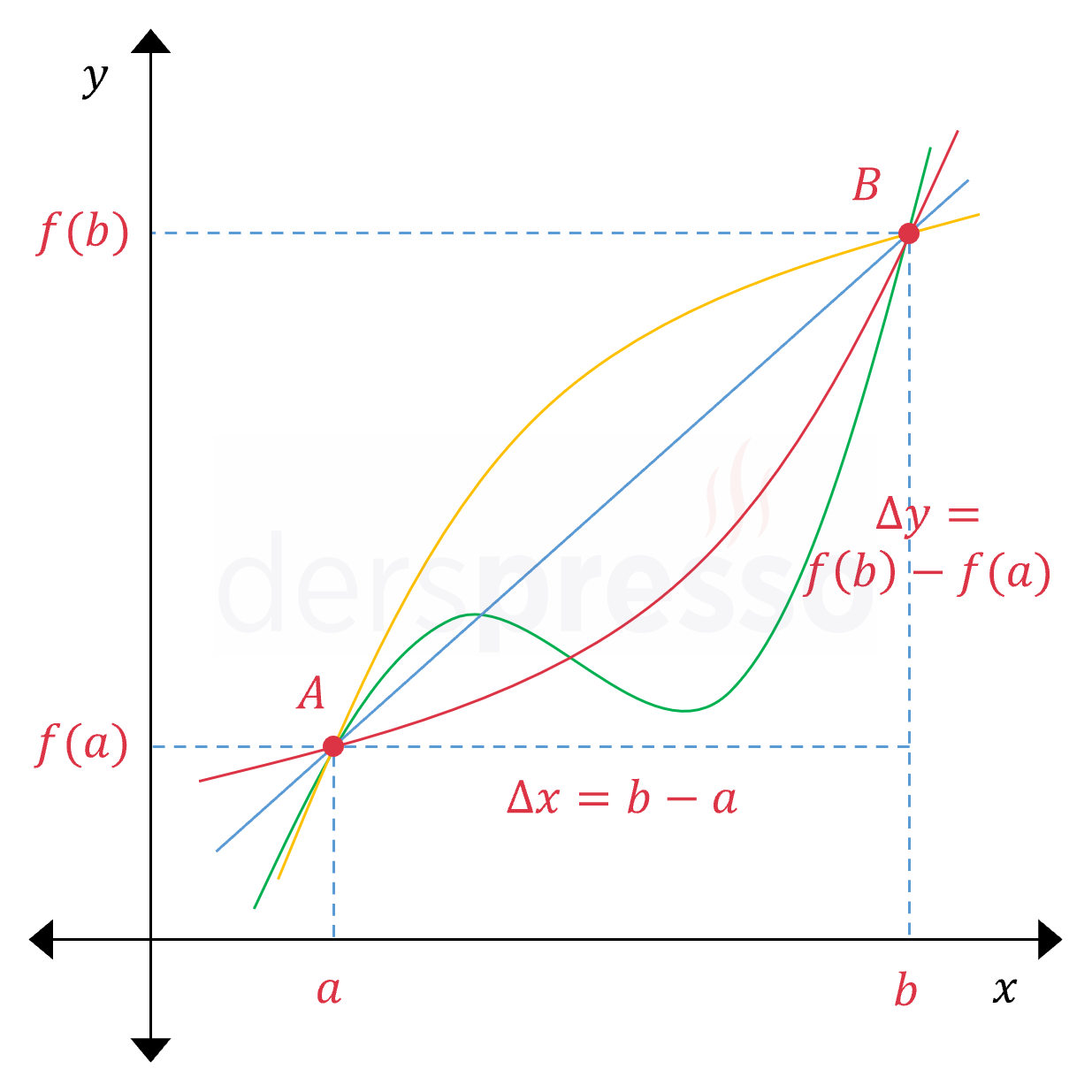
Değişim oranı pozitif, negatif ya da sıfır olabilir. Analitik düzlemde bu üç durum aşağıdaki şekillerde olabilir.

• $$ artarken $$ de artıyorsa değişim oranı pozitif olur.
• $$ artarken $$ azalıyorsa değişim oranı negatif olur.
• $$ artarken $$ değişmiyorsa değişim oranı sıfır olur.

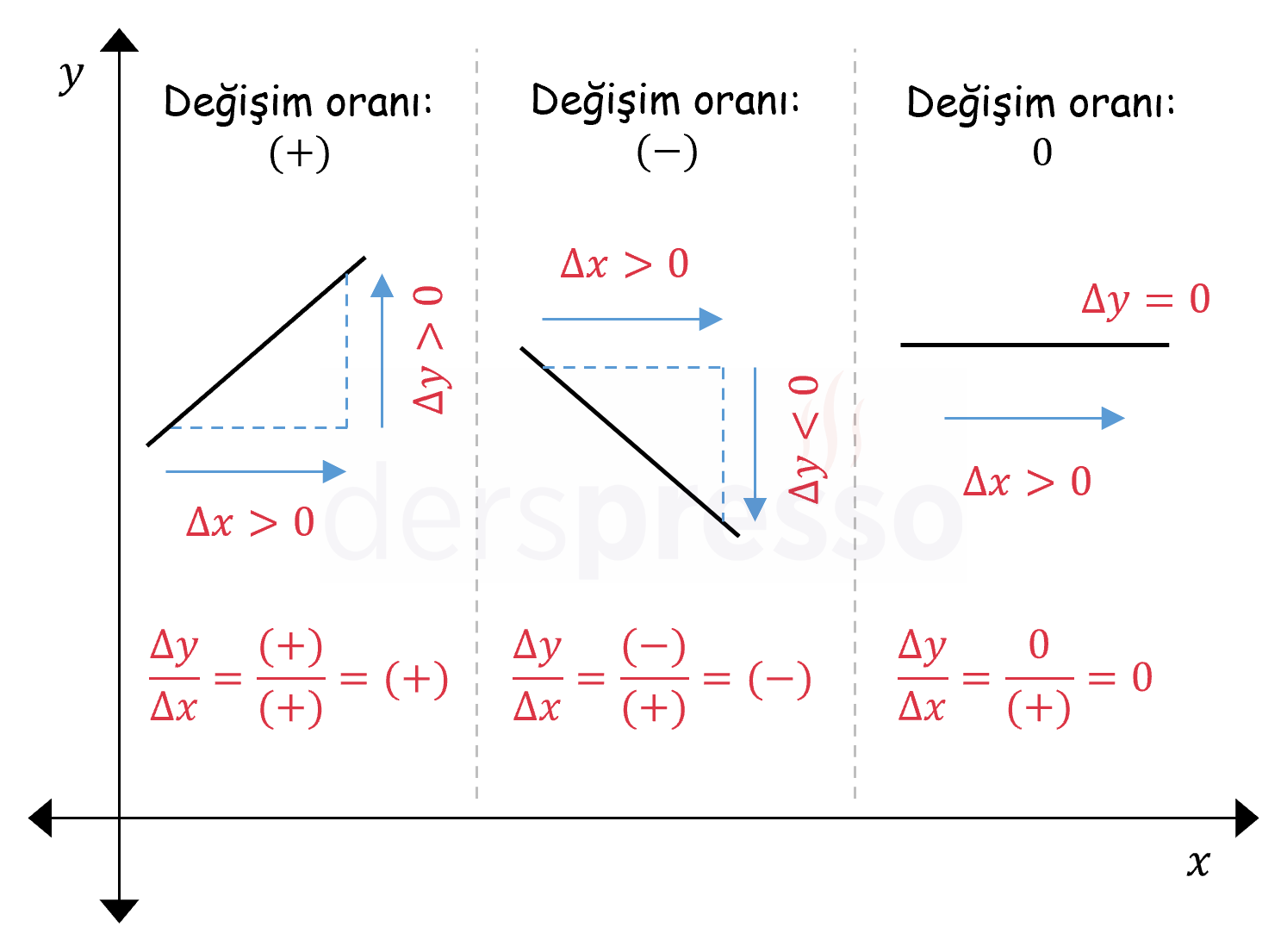
Ortalama değişim oranına aşağıdaki örnekleri verebiliriz.

• Bir aracın saatteki ortalama hızı (katedilen toplam mesafe bölü saat olarak geçen süre)
• Bir ülkenin nüfusundaki yıllık ortalama artış oranı (nüfustaki artış miktarı bölü yıl sayısı)
• Aylık ortalama enflasyon oranı (fiyatlardaki net değişim bölü ay sayısı)
• Bir ağacın boyunun yıllık ortalama büyüme hızı (ağacın boyundaki artış miktarı bölü yıl sayısı)
• Bir buzdolabının günlük ortalama elektrik tüketimi (toplam elektrik tüketimi bölü gün sayısı)

Anlık Değişim Oranı

Bir fonksiyonun belirli bir aralıktaki ortalama değişim oranı faydalı bir bilgi olsa da fonksiyonun belirli bir noktadaki davranışını açıklamaz. Örneğin bir otomobilin iki şehir arasındaki ortalama hızını 90 km/s olarak hesaplayabiliriz, ancak bu değer yolculuğun belirli bir anındaki hız hakkında bilgi vermez. Bu sebeple bir aralıktaki ortalama değişim oranına ek olarak belirli bir andaki değişim oranı da ek bir bilgi ihtiyacı olarak karşımıza çıkmaktadır. Bir fonksiyonun belirli bir noktadaki değişim oranına o noktadaki anlık değişim oranı denir.

Bir fonksiyonun belirli bir noktadaki anlık değişim oranı, fonksiyona o noktada çizilen teğet doğrunun eğimine eşittir. Örneğin aşağıda grafiği verilen fonksiyonun $$ noktasındaki anlık değişim oranı, fonksiyona bu noktada teğet olan $$ doğrusunun eğimine eşittir.

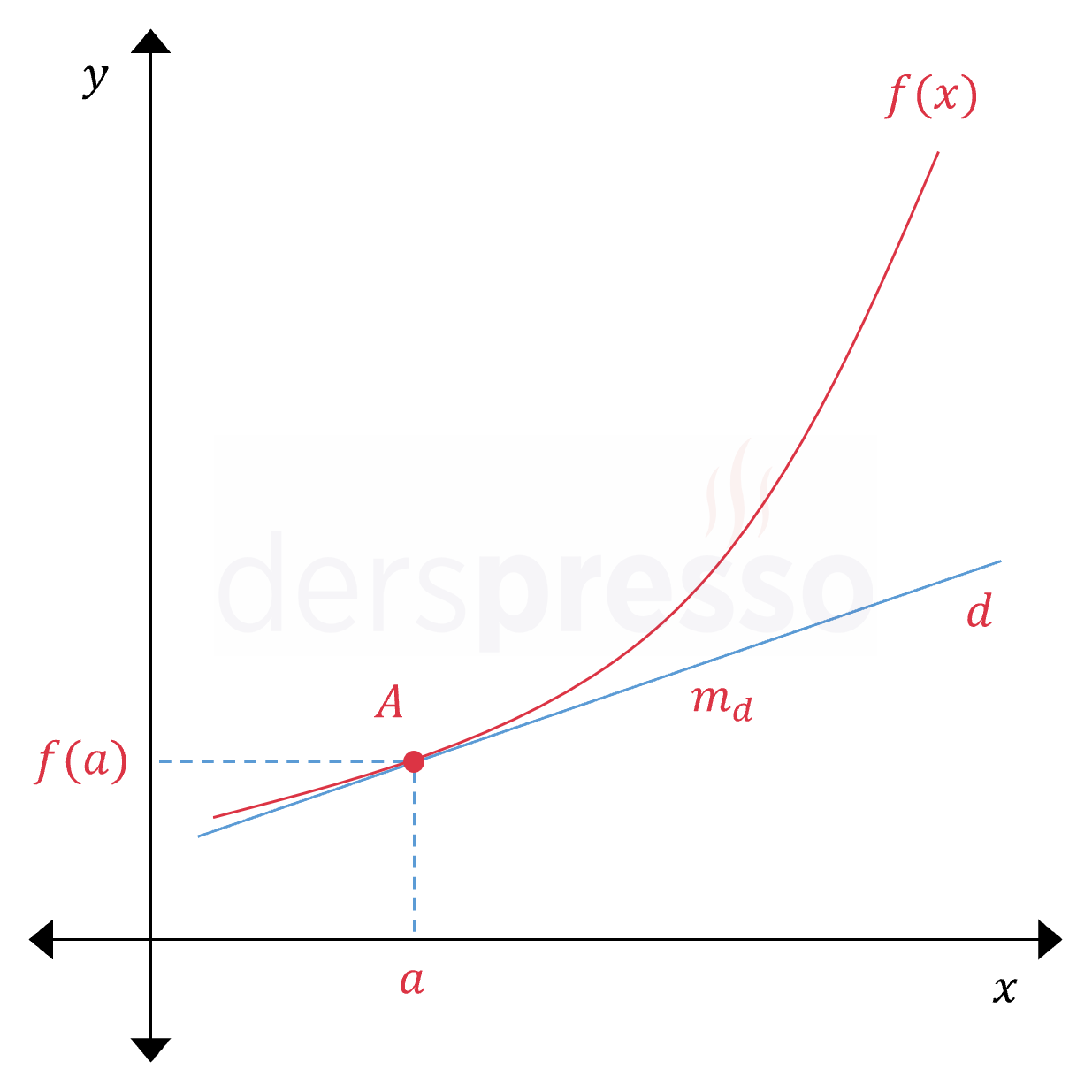
Önümüzdeki bölümlerde inceleyeceğimiz üzere, türevin ana amacı bir fonksiyonun belirli bir noktadaki anlık değişim oranını ve bu orana eşit olan fonksiyona bu noktada teğet olan doğrunun eğimini hesaplamaktır.