Teğet ve Normal Doğru Uygulamaları
Bir fonksiyonun belirli bir noktada türevlenebilir olması, fonksiyon grafiğine bu noktada bir teğet doğru çizilebilmesi anlamına gelir. Çizilen bu teğet doğrunun eğimi fonksiyonun bu noktadaki birinci türev değerine eşittir.
Bir fonksiyon bir noktada türevlenebilir ise bu noktadaki teğet doğrusuna aynı noktada dik olan doğruya fonksiyonun o noktadaki normali denir.
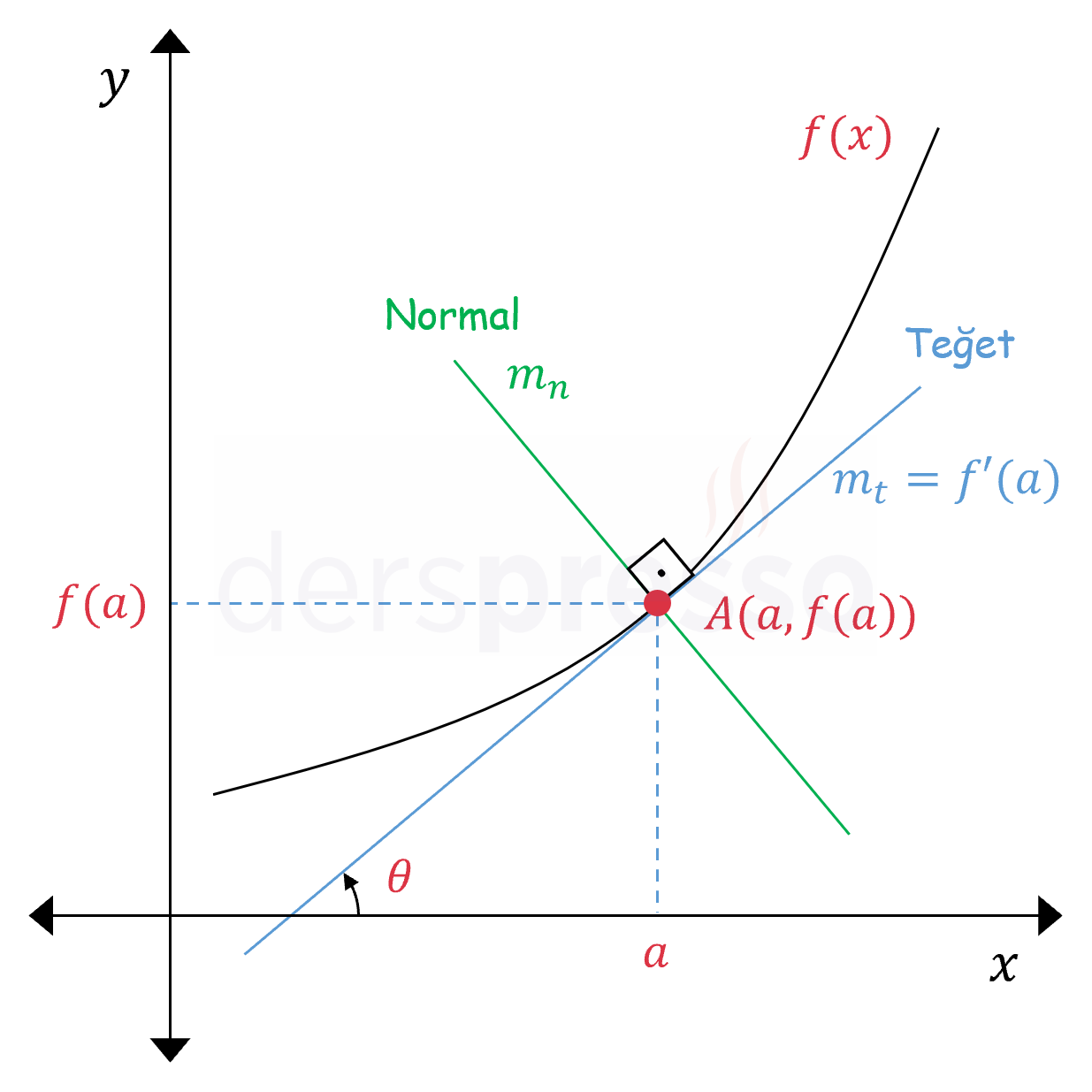
\( m_t = f'(a) = \tan{\theta} \)
Bir fonksiyonun bir noktadaki teğet ve normal doğruları birbirine dik oldukları için eğimleri çarpımı \( -1 \) olur.
\( m_t \cdot m_n = -1 \)
\( f'(a) \cdot m_n = -1 \)
\( m_n = -\dfrac{1}{f'(a)} \)
Buna göre bir \( f \) fonksiyonuna \( (a, f(a)) \) noktasında çizilen teğet doğrunun denklemini bir noktası ve eğimi bilinen doğru denklem formülü ile aşağıdaki şekilde yazabiliriz.
\( y - f(a) = f'(a)(x - a) \)
\( f \) fonksiyonuna \( (a, f(a)) \) noktasında çizilen normal doğrunun denklemi de aşağıdaki gibi olur.
\( y - f(a) = -\dfrac{1}{f'(a)}(x - a) \)
\( (a, f(a)) \) noktası hem ana fonksiyon, hem teğet doğru hem de normal doğrunun üzerinde olduğu için üç denklemi de sağlar.
Aşağıdaki her fonksiyon için, fonksiyon grafiğine belirtilen noktada çizilen teğet doğrunun denklemini bulunuz.
(a) \( f(x) = x^3 + 3x^2 - 4x - 7, \quad x = -1 \)
(b) \( g(x) = 2\sqrt{x} - \dfrac{9}{\sqrt{x}}, \quad x = 4 \)
(c) \( h(x) = 2\sqrt{x^5} - \dfrac{7}{x}, \quad x = 1 \)
Çözümü GösterBir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyona o noktada teğet olan doğrunun eğimini verir.
Bir fonksiyona \( x = a \) noktasında çizilen teğet doğrunun denklemi aşağıdaki formülle bulunur.
\( y - f(a) = f'(a)(x - a) \)
(a) seçeneği:
\( f(x) = x^3 + 3x^2 - 4x - 7, \quad x = -1 \)
Fonksiyonun \( x = -1 \) noktasındaki ordinat değerini bulalım.
\( f(-1) = (-1)^3 + 3(-1)^2 - 4(-1) - 7 = -1 \)
\( x = -1 \) noktasındaki türev değerini bulalım.
\( f'(x) = 3x^2 + 6x - 4 \)
\( f'(-1) = 3(-1)^2 + 6(-1) - 4 = -7 \)
\( (-1, -1) \) noktasından geçen ve eğimi \( -7 \) olan teğet doğrunun denklemini yazalım.
\( y - f(a) = f'(a)(x - a) \)
\( y - (-1) = -7(x - (-1)) \)
\( y = -7x - 8 \)
(b) seçeneği:
\( g(x) = 2\sqrt{x} - \dfrac{9}{\sqrt{x}}, \quad x = 4 \)
Fonksiyonun \( x = 4 \) noktasındaki ordinat değerini bulalım.
\( g(4) = 2\sqrt{4} - \dfrac{9}{\sqrt{4}} = -\dfrac{1}{2} \)
\( x = 4 \) noktasındaki türev değerini bulalım.
\( g'(x) = \dfrac{1}{\sqrt{x}} + \dfrac{9}{2\sqrt{x^3}} \)
\( g'(4) = \dfrac{1}{\sqrt{4}} + \dfrac{9}{2\sqrt{4^3}} = \dfrac{17}{16} \)
\( (4, -\frac{1}{2}) \) noktasından geçen ve eğimi \( \frac{17}{16} \) olan teğet doğrunun denklemini yazalım.
\( y - f(a) = f'(a)(x - a) \)
\( y - (-\dfrac{1}{2}) = \dfrac{17}{16}(x - 4) \)
\( y = \dfrac{17}{16}x - \dfrac{19}{4} \)
(c) seçeneği:
\( h(x) = 2\sqrt{x^5} - \dfrac{7}{x}, \quad x = 1 \)
Fonksiyonun \( x = 1 \) noktasındaki ordinat değerini bulalım.
\( h(1) = 2\sqrt{1^5} - \dfrac{7}{1} = -5 \)
\( x = 1 \) noktasındaki türev değerini bulalım.
\( h'(x) = 5\sqrt{x^3} + \dfrac{7}{x^2} \)
\( h'(1) = 5\sqrt{1^3} + \dfrac{7}{1^2} = 12 \)
\( (1, -5) \) noktasından geçen ve eğimi 12 olan teğet doğrunun denklemini yazalım.
\( y - f(a) = f'(a)(x - a) \)
\( y - (-5) = 12(x - 1) \)
\( y = 12x - 17 \)
Aşağıdaki her fonksiyon için, fonksiyon grafiğine belirtilen noktada çizilen normal doğrunun denklemini bulunuz.
(a) \( f(x) = 2x^3 - 4x^2 - 10x + 6, \quad x = 2 \)
(b) \( g(x) = \dfrac{1}{3}x^4 - 30x + 60, \quad x = 3 \)
(c) \( h(x) = x^3(x - 1) + \dfrac{7}{x} + 5, \quad x = 1 \)
Çözümü GösterBir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyona o noktada teğet olan doğrunun eğimini verir.
Bir fonksiyona \( x = a \) noktasında çizilen normal doğrunun denklemi aşağıdaki formülle bulunur.
\( y - f(a) = -\dfrac{1}{f'(a)}(x - a) \)
(a) seçeneği:
\( f(x) = 2x^3 - 4x^2 - 10x + 6, \quad x = 2 \)
Fonksiyonun \( x = 2 \) noktasındaki ordinat değerini bulalım.
\( f(2) = 2(2)^3 - 4(2)^2 - 10(2) + 6 = -14 \)
\( x = 2 \) noktasındaki türev değerini bulalım.
\( f'(x) = 6x^2 - 8x - 10 \)
\( f'(2) = 6(2)^2 - 8(2) - 10 = -2 \)
\( (2, -14) \) noktasından geçen ve eğimi \( -2 \) olan teğet doğruya dik olan normal doğrunun denklemini yazalım.
\( y - f(a) = -\dfrac{1}{f'(a)}(x - a) \)
\( y - (-14) = -\dfrac{1}{-2}(x - 2) \)
\( y = \dfrac{1}{2}x - 15 \)
(b) seçeneği:
\( g(x) = \dfrac{1}{3}x^4 - 30x + 60, \quad x = 3 \)
Fonksiyonun \( x = 3 \) noktasındaki ordinat değerini bulalım.
\( g(3) = \dfrac{1}{3}3^4 - 30(3) + 60 = -3 \)
\( x = 3 \) noktasındaki türev değerini bulalım.
\( g'(x) = \dfrac{4}{3}x^3 - 30 \)
\( g'(3) = \dfrac{4}{3}3^3 - 30 = 6 \)
\( (3, -3) \) noktasından geçen ve eğimi 6 olan teğet doğruya dik olan normal doğrunun denklemini yazalım.
\( y - f(a) = -\dfrac{1}{f'(a)}(x - a) \)
\( y - (-3) = -\dfrac{1}{6}(x - 3) \)
\( y = -\dfrac{1}{6}x - \dfrac{5}{2} \)
(c) seçeneği:
\( h(x) = x^3(x - 1) + \dfrac{7}{x} + 5, \quad x = 1 \)
Fonksiyonun \( x = 1 \) noktasındaki ordinat değerini bulalım.
\( h(1) = 1^3(1 - 1) + \dfrac{7}{1} + 5 = 12 \)
\( x = 1 \) noktasındaki türev değerini bulalım.
\( h(x) = x^4 - x^3 + \dfrac{7}{x} + 5, \quad x = 1 \)
\( h'(x) = 4x^3 - 3x^2 - \dfrac{7}{x^2} \)
\( h'(1) = 4(1)^3 - 3(1)^2 - \dfrac{7}{1^2} = -6 \)
\( (1, 12) \) noktasından geçen ve eğimi \( -6 \) olan teğet doğruya dik olan normal doğrunun denklemini yazalım.
\( y - f(a) = -\dfrac{1}{f'(a)}(x - a) \)
\( y - 12 = -\dfrac{1}{-6}(x - 1) \)
\( y = \dfrac{1}{6}x + \dfrac{71}{6} \)
\( f(x) = x^3 - 19x + 4 \) eğrisi üzerinde eğimi 8 olan noktaların koordinatlarını bulunuz.
Çözümü GösterBir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyona o noktada teğet olan doğrunun eğimini verir.
\( f'(x) = (x^3 - 19x + 4)' \)
\( = 3x^2 - 19 \)
Eğri üzerinde eğimi 8 olan noktaları bulabilmek için birinci türevi 8'e eşitleyelim.
\( f'(x) = 3x^2 - 19 = 8 \)
\( x^2 = 9 \)
\( x \in \{-3, 3\} \)
Bulduğumuz \( x \) değerlerini fonksiyonda yerine koyarak bu noktaların ordinat değerlerini bulalım.
\( f(-3) = (-3)^3 - 19(-3) + 4 = 34 \)
\( f(3) = 3^3 - 19(3) + 4 = -26 \)
Eğri üzerinde koordinatları \( (-3, 34) \) ve \( (3, -26) \) olan noktalarda eğriye çizilen teğet doğruların eğimi 8 olur.
\( f(x) = \frac{1}{3}x^3 + 4x^2 + 29x \) eğrisi üzerindeki hangi noktalarda çizilen teğet doğrular \( 2y = 26x + 5 \) doğrusuna paraleldir?
Çözümü GösterEğriye bir noktada çizilen teğet doğrunun verilen doğruya paralel olması için iki doğrunun eğimleri eşit olmalıdır.
\( y = mx + c \) formundaki bir doğru denkleminde \( m \) katsayısı doğrunun eğimini verir.
\( 2y = 26x + 5 \) denklemini \( y = mx + c \) formunda yazalım.
\( y = 13x + \dfrac{5}{2} \)
Buna göre doğrunun eğimi 13 olur.
Bir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyona o noktada teğet olan doğrunun eğimini verir.
\( f'(x) = x^2 + 8x + 29 \)
Fonksiyonun birinci türevinin (eğiminin) 13 olduğu noktaları bulalım.
\( f'(x) = x^2 + 8x + 29 = 13 \)
\( x^2 + 8x + 16 = 0 \)
\( (x + 4)^2 = 0 \)
\( x = -4 \)
\( f(-4) = \dfrac{1}{3}(-4)^3 + 4(-4)^2 + 29(-4) = -\dfrac{220}{3} \)
Buna göre fonksiyona sadece \( (-4, -\frac{220}{3} ) \) noktasında çizilen teğet doğru \( 2y = 26x + 5 \) doğrusuna paraleldir.
\( f(x) = ax^3 + bx^2 + 5 \) eğrisine \( P(2, 7) \) noktasında çizilen teğet doğrunun eğimi 4 olduğuna göre, \( a \cdot b \) kaçtır?
Çözümü Göster\( P(2, 7) \) noktası verilen eğri üzerinde olduğuna göre, koordinatları denklemi sağlar.
\( f(2) = a(2)^3 + b(2)^2 + 5 = 7 \)
\( 8a + 4b + 5 = 7 \)
\( 2a + b = \dfrac{1}{2} \)
\( P(2, 7) \) noktasında çizilen teğet doğrunun eğimi 4'tür.
\( f'(x) = 3ax^2 + 2bx \)
\( f'(2) = 3a(2)^2 + 2b(2) = 4 \)
\( 12a + 4b = 4 \)
\( 3a + b = 1 \)
Bulduğumuz iki bilinmeyenli iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = \dfrac{1}{2}, \quad b = -\dfrac{1}{2} \)
\( a \cdot b = \dfrac{1}{2} \cdot (-\dfrac{1}{2}) = -\dfrac{1}{4} \) bulunur.
\( f(x) = \cos^2{x} \) fonksiyon grafiğini \( x = \frac{\pi}{4} \) noktasında kesen teğetin denklemini yazınız.
Çözümü GösterBir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyonun o noktadaki teğetinin eğimini verir.
\( f'(x) = 2\cos{x}(\cos{x})' \)
\( = -2\cos{x}\sin{x} \)
Sinüs iki kat açı formülünü kullanalım.
\( = -\sin(2x) \)
\( x = \frac{\pi}{4} \) noktasındaki türev değerini bulalım.
\( f'(\dfrac{\pi}{4}) = -\sin(2 \cdot \dfrac{\pi}{4}) = -1 \)
Fonksiyonun \( x = \frac{\pi}{4} \) noktasındaki ordinat değerini bulalım.
\( f(\dfrac{\pi}{4}) = \cos^2{\dfrac{\pi}{4}} = \dfrac{1}{2} \)
\( (\frac{\pi}{4}, \frac{1}{2}) \) noktasından geçen ve eğimi \( -1 \) olan doğrunun denklemini yazalım.
\( y - y_1 = f'(x_1)(x - x_1) \)
\( y - \dfrac{1}{2} = -1(x - \dfrac{\pi}{4}) \)
\( y - \dfrac{1}{2} = -x + \dfrac{\pi}{4} \)
\( y = -x + \dfrac{\pi + 2}{4} \) olarak bulunur.
\( f(x) = \cos(3x) \) fonksiyonunun apsisi \( x = \frac{\pi}{6} \) olan noktasından geçen normalinin eğimi nedir?
Çözümü GösterBir fonksiyonun birinci türevi o fonksiyonun herhangi bir noktasındaki teğetinin eğimini verir.
\( f'(x) = -\sin(3x) \cdot (3x)' \)
\( = -3\sin(3x) \)
Fonksiyonun \( A \) noktasındaki teğetinin eğimini bulmak için türev fonksiyonunda \( x = \frac{\pi}{6} \) koyalım.
\( f'(\frac{\pi}{6}) = -3\sin(3 \cdot \frac{\pi}{6}) = -3 \)
Fonksiyonun bir noktadaki normali o noktadaki teğetine dik olan doğrudur, dolayısıyla bu noktadaki normalin eğimi (\( m_n \)) ile teğetin eğiminin (\( m_t \)) çarpımı \( -1 \) olur.
\( m_t \cdot m_n = -1 \)
\( -3 \cdot m_n = -1 \)
Bu noktadaki normalin eğimi \( m_n = \frac{1}{3} \) olarak bulunur.
\( f(x) = x^3 - ax^2 + bx - 4 \) eğrisinin apsisi \( x = -1 \) olan noktasındaki teğetinin denklemi \( y = 3x + 5 \) olduğuna göre, \( a \cdot b \) kaçtır?
Çözümü GösterBir fonksiyonun birinci türevi o fonksiyonun herhangi bir noktasındaki teğetinin eğimini verir.
\( f'(x) = 3x^2 - 2ax + b \)
Fonksiyonun apsisi \( x = -1 \) olan noktasındaki teğetinin eğimini bulmak için \( x = -1 \) koyalım.
\( f'(-1) = 3(-1)^2 - 2a(-1) + b = 2a + b + 3 \)
Bu eğim değeri teğet doğrunun eğimi olan 3'e eşittir.
\( 2a + b + 3 = 3 \)
\( 2a + b = 0 \)
\( f \) fonksiyonu ve doğru apsisi \( x = -1 \) olan noktada kesiştikleri için bu noktanın koordinatları iki denklemi de sağlamalıdır.
\( y = 3(-1) + 5 = 2 \)
Buna göre doğru fonksiyona \( (-1, 2) \) noktasında teğettir. Bu noktanın koordinatları \( f \) fonksiyonunu da sağlamalıdır.
\( f(-1) = 2 \)
\( (-1)^3 - a(-1)^2 + b(-1) - 4 = 2 \)
\( -1 - a - b - 4 = 2 \)
\( a + b = -7 \)
\( a \) ve \( b \) bilinmeyenlerinden oluşan iki denklemi ortak çözelim.
\( a = 7, \quad b = -14 \)
Buna göre \( a \cdot b = -98 \) bulunur.
\( f(x) = x^2 - 7x \) fonksiyonunun hangi noktasındaki teğeti \( y = -x + 4 \) doğrusuna diktir?
Çözümü Göster\( y = -x + 4 \) doğrusunun eğimi \( -1 \)'dir. Birbirine dik olan iki doğrunun eğimleri çarpımı \( -1 \) olduğu için dik doğrunun eğimi \( 1 \) olur.
Bir fonksiyonun birinci türevi o fonksiyonun herhangi bir noktasındaki teğetinin eğimini verir.
\( f'(x) = 2x - 7 \)
\( f \) fonksiyonunun eğim değerinin \( 1 \) olduğu noktaya \( (a, f(a)) \) diyelim.
\( f'(a) = 1 \)
\( 2a - 7 = 1 \)
\( a = 4 \)
Buna göre fonksiyonun apsisi \( x = 4 \) olan noktadaki teğetinin eğimi 1 olur.
Bu noktanın ordinat değerini bulmak için \( f \) fonksiyonunda \( x = 4 \) koyalım.
\( f(4) = 4^2 - 7(4) = -12 \)
Buna göre fonksiyonun \( (4, -12) \) noktasındaki teğeti \( y = -x + 4 \) doğrusuna diktir.
\( f(x) = x^2 + ax + b \) eğrisine üzerindeki \( A(1, 2) \) noktasından çizilen teğet \( x \) eksenine paralel olduğuna göre, \( a \cdot b \) nedir?
Çözümü Göster\( A(1, 2) \) noktası \( f(x) = x^2 + ax + b \) eğrisi üzerinde olduğuna göre bu noktanın koordinatları denklemi sağlar.
\( f(1) = 2 \)
\( 1^2 + a(1) + b = 2 \)
\( a + b = 1 \)
Bir fonksiyonun birinci türevi o fonksiyonun herhangi bir noktasındaki teğetinin eğimini verir.
\( f'(x) = 2x + a \)
\( A(1, 2) \) noktasındaki teğet \( x \) eksenine paralel olduğuna göre bu teğet doğrunun eğimi 0 olur.
\( f'(1) = 0 \)
\( 2(1) + a = 0 \)
\( a = -2 \)
\( a + b = 1 \Longrightarrow b = 3 \)
Buna göre \( a \cdot b = -2 \cdot 3 = -6 \) bulunur.
\( y = x^3 + c \) ve \( y^2 = x \) denklemleri tek bir noktada kesiştiklerine göre, \( c \) kaçtır?
Çözümü Gösterİki eğri tek bir noktada kesişiyorsa bu noktada eğimleri (birinci türevleri) eşittir.
İkinci denklemde \( y \)'yi yalnız bırakalım.
\( y = \sqrt{x} \)
Denklemlerin türevlerini birbirine eşitleyelim.
\( 3x^2 = \dfrac{1}{2\sqrt{x}} \)
\( x^{\frac{5}{2}} = \dfrac{1}{6} \)
\( x = 6^{-\frac{2}{5}} \)
İki eğrinin kesiştikleri noktada apsis ve ordinat değerleri de eşit olur.
\( x^3 + c = \sqrt{x} \)
\( (6^{-\frac{2}{5}})^3 + c = (6^{-\frac{2}{5}})^{\frac{1}{2}} \)
\( 6^{-\frac{6}{5}} + c = 6^{-\frac{1}{5}} \)
\( c = 6^{-\frac{1}{5}} - 6^{-\frac{6}{5}} \)
\( = 6^{-\frac{1}{5}}(1 - 6^{-1}) \)
\( = \dfrac{5}{6\sqrt[5]{6}} = \dfrac{5\sqrt[5]{6^4}}{36} \) olarak bulunur.
\( f: [0, 2\pi) \to \mathbb{R} \) olmak üzere,
\( f(x) = e^{\cos{x}} \) fonksiyonunun hangi apsisli noktasındaki teğetinin eğimi o noktadaki fonksiyon değerine eşit olur?
Çözümü GösterFonksiyonun türevini alalım.
\( f'(x) = (e^{\cos{x}})' \)
\( = e^{\cos{x}} \cdot (\cos{x})' \)
\( = -e^{\cos{x}} \cdot \sin{x} \)
Eğimin fonksiyon değerine eşit olduğu noktaya \( x = a \) diyelim. Bu noktayı bulmak için ana fonksiyonu türev fonksiyonuna eşitleyelim.
\( f(a) = f'(a) \)
\( e^{\cos{a}} = -e^{\cos{a}} \cdot \sin{a} \)
\( 1 = -\sin{a} \)
\( \sin{a} = -1 \)
Sinüs fonksiyonu \( [0, 2\pi) \) aralığında -1 değerini \( x = \frac{3\pi}{2} \) noktasında alır.
Buna göre \( f \) fonksiyonunun \( x = \frac{3\pi}{2} \) apsisli noktada eğimi fonksiyon değerine eşit olur.
\( f(x) = x^7 + 6x^3 + 3x \) eğrisinin eğimi en küçük olan teğetinin eğimi kaçtır?
Çözümü GösterBir fonksiyonunun birinci türevi fonksiyona belirli bir noktada teğet olan doğrunun eğimini verir.
En küçük eğim değerini bulmak için \( f(x) \) fonksiyonunun türevini alalım.
\( f'(x) = 7x^6 + 18x^2 + 3 \)
Bir sayının çift sayı kuvvetleri her zaman pozitif olacağından birinci türev minimum değerini \( x = 0 \) olduğunda alacaktır.
Türev fonksiyonunda \( x = 0 \) yazalım.
\( f'(0) = 7(0)^6 + 18(0)^2 + 3 = 3 \)
Buna göre fonksiyonun eğimi en küçük olan teğetinin eğimi 3 olarak bulunur.
\( f(x) = 3x^3 + 5x^2 - 17 \) fonksiyonuna çizilen teğetlerden eğimi en küçük olanın eğimi kaçtır?
Çözümü Göster\( f \) fonksiyonunun belirli bir noktadaki eğimini bulmak için fonksiyonun türevini alalım.
\( f'(x) = 9x^2 + 10x \)
En küçük eğim değerini bulmak için birinci türev fonksiyonunun mutlak minimum noktasını bulmalıyız. Pozitif başkatsayılı (kolları yukarı yönlü) ikinci dereceden polinom fonksiyonu için bu nokta birinci türev grafiğinin eğiminin sıfır olduğu tepe noktasıdır.
Bu noktayı bulmak için ikinci türev fonksiyonunun sıfıra eşit olduğu noktayı bulalım.
\( f''(x) = 18x + 10 = 0 \)
\( x = -\dfrac{5}{9} \)
Eğimin en küçük değerini aldığı bu noktayı birinci türevde yerine yazıp eğim değerini bulalım.
\( f'(-\frac{5}{9}) = 9(-\frac{5}{9})^2 + 10(-\frac{5}{9}) \)
\( = -\dfrac{25}{9} \) bulunur.
\( f(x) = x^3 - 4x^2 + 4x - 3 \) eğrisine üzerindeki \( P(2, -3) \) noktasında çizilen teğet doğruya paralel olan ve eğriye ikinci bir noktada teğet olan doğrunun denklemini bulunuz.
Çözümü GösterÖnce eğriye \( P(2, -3) \) noktasında teğet olan doğrunun eğimini bulalım.
Bir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyona o noktada teğet olan doğrunun eğimini verir.
\( f'(x) = 3x^2 - 8x + 4 \)
\( f'(2) = 3(2)^2 - 8(2) + 4 = 0 \)
Buna göre eğriye \( P(2, -3) \) noktasında teğet olan doğrunun eğimi sıfırdır, yani doğru yataydır.
Buna göre bu doğruya paralel olan ikinci doğrunun eğimi de sıfır olur.
Eğimi sıfır olan ve eğriye teğet olan tüm doğruların apsis değerlerini bulmak için eğrinin birinci türevini sıfıra eşitleyelim.
\( f'(x) = 3x^2 - 8x + 4 = 0 \)
\( (3x - 2)(x - 2) = 0 \)
\( x \in \{\frac{2}{3}, 2\} \)
\( x = 2 \) apsisli nokta \( P \) noktasıdır. Buna göre soruda istenen ikinci doğrunun eğriye teğet olduğu noktanın apsis değeri \( x = \frac{2}{3} \) olur.
Bu noktanın ordinat değerini bulalım.
\( f(\dfrac{2}{3}) = (\dfrac{2}{3})^3 - 4(\dfrac{2}{3})^2 + 4\dfrac{2}{3} - 3 = -\dfrac{49}{27} \)
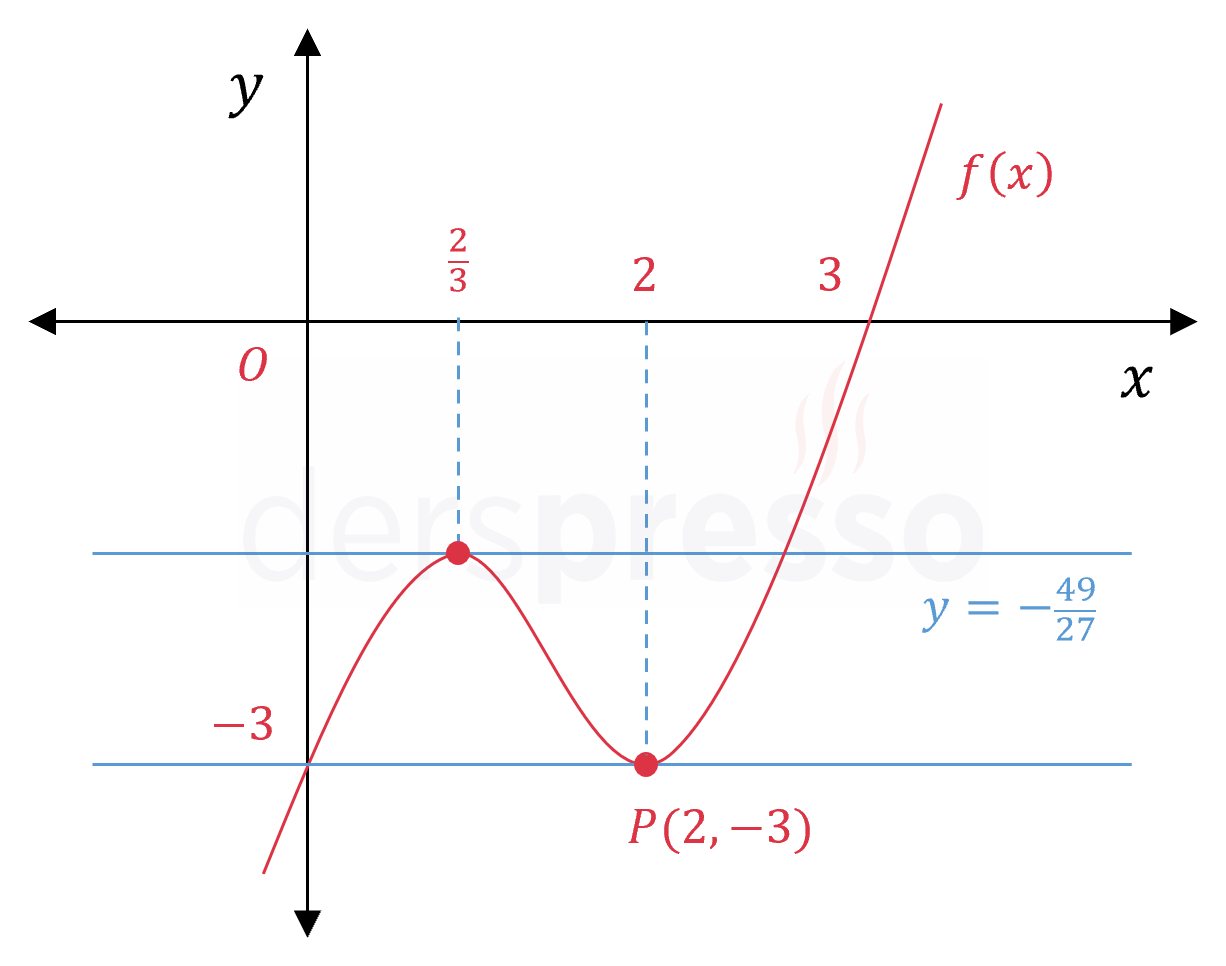
\( (\frac{2}{3}, -\frac{49}{27}) \) noktasından geçen ve eğimi 0 olan doğrunun denklemi aşağıdaki gibidir.
\( y = -\dfrac{49}{27} \)
Fonksiyonun ve teğet doğruların grafikleri aşağıdaki şekilde verilmiştir.
\( f(x) = (2x - 3)^4 \) eğrisine teğet ve \( 8y = x \) doğrusuna dik olan \( L \) doğrusunun denklemini yazınız.
Çözümü Göster\( y = \dfrac{1}{8}x \)
\( L \) doğrusunun eğimine \( m_L \) diyelim.
Birbirini dik kesen doğruların eğimleri çarpımı -1'dir.
\( \dfrac{1}{8} \cdot m_L = -1 \)
\( m_L = -8 \)
Bir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyona o noktada teğet olan doğrunun eğimini verir.
\( f'(x) = 4(2x - 3)^3(2x - 3)' \)
\( = 8(2x - 3)^3 \)
Eğri üzerinde eğimi -8 olan noktayı bulmak için birinci türevi bu değere eşitleyelim.
\( f'(x) = 8(2x - 3)^3 = -8 \)
\( (2x - 3)^3 = -1 \)
\( 2x - 3 = -1 \)
\( x = 1 \)
\( f \) fonksiyonunda \( x = 1 \) koyarak bu noktanın ordinat değerini bulalım.
\( f(1) = (2(1) - 3)^4 = 1 \)
Buna göre \( L \) doğrusu \( f \) fonksiyonuna \( (1, 1) \) noktasında teğettir.
Bir noktası ve eğimi bilinen doğrunun denklemini yazalım.
\( y - f(1) = m_L(x - 1) \)
\( y - 1 = -8(x - 1) \)
\( y = -8x + 9 \) olarak bulunur.
\( a \in \mathbb{R} \) olmak üzere,
\( f(x) = 4x^2 \) parabolüne \( x = a \) noktasında çizilen teğet doğru \( (1, -5) \) noktasından geçiyor.
Buna göre \( a \)'nın alabileceği değerler toplamı kaçtır?
Çözümü Gösterİstenen noktanın apsis değerine \( x = a \) diyelim.
Bir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyona o noktada teğet olan doğrunun eğimini verir.
\( f'(x) = 8x \)
\( x = a \) noktasındaki eğim değerini bulalım.
\( f'(a) = 8a \)
Teğet doğrunun \( (a, f(a)) \) ve \( (1, -5) \) noktalarından geçtiği ve eğiminin \( 8a \) olduğu biliniyor.
Eğim formülü ile iki noktadan geçen doğrunun eğimini hesaplayalım.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( 8a = \dfrac{-5 - f(a)}{1 - a} \)
\( f(a) = 4a^2 \) yazalım.
\( 8a = \dfrac{-5 - 4a^2}{1 - a} \)
Denklemi çözelim.
\( -5 - 4a^2 = 8a - 8a^2 \)
\( 4a^2 - 8a - 5 = 0 \)
\( (2a + 1)(2a - 5) = 0 \)
Buna göre \( f \) parabolüne \( a = -\frac{1}{2} \) ve \( a = \frac{5}{2} \) apsisli noktalarda çizilen teğet doğrular \( (1, -5) \) noktasından geçer.
\( -\dfrac{1}{2} + \dfrac{5}{2} = 2 \) bulunur.
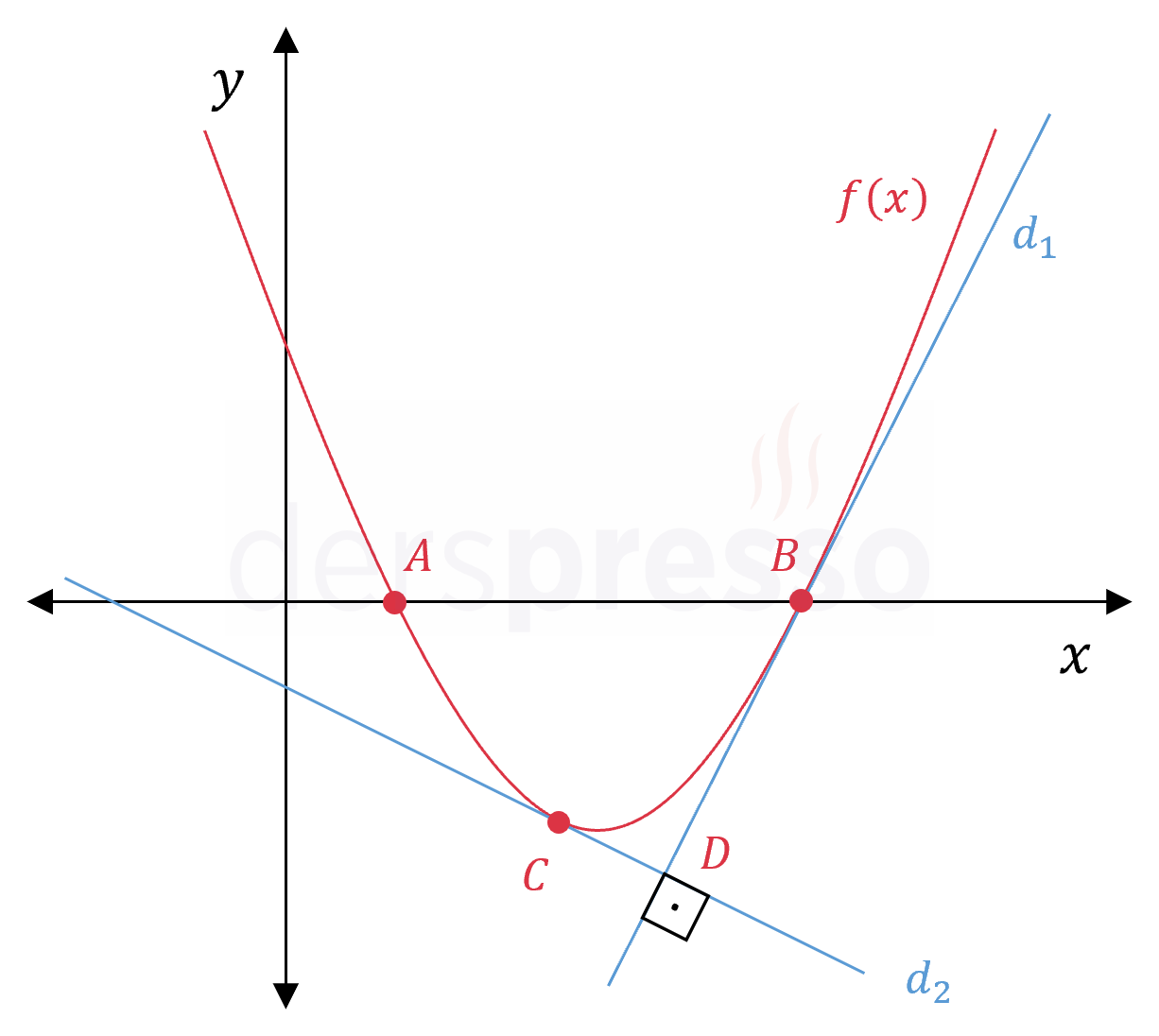
Yukarıda \( f(x) = \dfrac{1}{2}x^2 - 3x + \dfrac{5}{2} \) parabolünün grafiği verilmiştir.
Parabolün \( B \) noktasındaki teğeti \( d_1 \), \( C \) noktasındaki teğeti \( d_2 \)'dir. Bu iki doğru \( D \) noktasında birbirini dik kesmektedir.
(a) \( d_1 \) doğrusunun denklemini bulunuz.
(b) \( d_2 \) doğrusunun denklemini bulunuz.
(c) \( D \) noktasının koordinatlarını bulunuz.
Çözümü Göster(a) seçeneği:
Önce parabolün \( x \) eksenini kestiği \( A \) ve \( B \) noktalarının koordinatlarını bulalım.
\( f(x) = \dfrac{1}{2}x^2 - 3x + \dfrac{5}{2} = 0 \)
\( \dfrac{1}{2}(x^2 - 6x + 5) = 0 \)
\( \dfrac{1}{2}(x - 1)(x - 5) = 0 \)
\( A(1, 0), \quad B(5, 0) \)
\( d_1 \) doğrusunun eğimini bulalım.
Bir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyona o noktada teğet olan doğrunun eğimini verir.
\( f'(x) = x - 3 \)
\( f'(5) = 5 - 3 = 2 \)
\( B(5, 0) \) noktasından geçen ve eğimi 2 olan \( d_1 \) doğrusunun denklemini bulalım.
\( y - f(5) = f'(5)(x - 5) \)
\( y - 0 = 2(x - 5) \)
\( d_1: y = 2x - 10 \)
(b) seçeneği:
\( C \) noktasının koordinatlarını bulalım.
\( d_1 \perp d_2 \) olduğu için iki doğrunun eğimleri çarpımı \( -1 \) olur.
\( d_1 \) doğrusunun eğimi 2 olduğundan \( d_2 \) doğrusunun eğimi \( -\frac{1}{2} \) olur.
\( d_2 \) doğrusunun eğimi \( -\frac{1}{2} \) ise eğrinin \( C \) noktasındaki birinci türevi bu değere eşit olur.
\( f'(x) = x - 3 = -\dfrac{1}{2} \)
\( x = \dfrac{5}{2} \)
\( C \) noktasının ordinat değerini bulalım.
\( f(\dfrac{5}{2}) = \dfrac{1}{2}(\dfrac{5}{2})^2 - 3(\dfrac{5}{2}) + \dfrac{5}{2} \)
\( = -\dfrac{15}{8} \)
\( C(\dfrac{5}{2}, -\dfrac{15}{8}) \)
\( C(\frac{5}{2}, -\frac{15}{8}) \) noktasından geçen ve eğimi \( -\frac{1}{2} \) olan \( d_2 \) doğrusunun denklemini bulalım.
\( y - f(\dfrac{5}{2}) = f'(\dfrac{5}{2})(x - \dfrac{5}{2}) \)
\( y - (-\dfrac{15}{8}) = -\dfrac{1}{2}(x - \dfrac{5}{2}) \)
\( d_2: y = -\dfrac{1}{2}x - \dfrac{5}{8} \)
(c) seçeneği:
\( d_1 \) ve \( d_2 \) doğrularının kesişimi olan \( D \) noktasının koordinatlarını bulmak için iki doğru denklemini ortak çözelim.
\( 2x - 10 = -\dfrac{1}{2}x - \dfrac{5}{8} \)
\( 16x - 80 = -4x - 5 \)
\( x = \dfrac{15}{4} \)
Bu apsis değerini doğru denklemlerinden birinde yerine koyalım.
\( y = 2(\dfrac{15}{4}) - 10 = -\dfrac{5}{2} \)
\( D(\frac{15}{4}, -\frac{5}{2}) \)
\( f(x) = x^3 - 2x + 2 \) eğrisine \( P(1, 1) \) noktasında çizilen teğet doğrunun eğriyi ikinci kez kestiği \( Q \) noktasının koordinatlarını bulunuz.
Çözümü GösterBir fonksiyonun birinci türevi o fonksiyonun herhangi bir noktasındaki teğetinin eğimini verir.
\( f'(x) = 3x^2 - 2 \)
\( f'(1) = 3(1)^2 - 2 = 1 \)
\( P(1, 1) \) noktasından geçen ve eğimi 1 olan teğet doğrunun denklemini bulalım.
\( y - f(1) = f'(1)(x - 1) \)
\( y - 1 = 1(x - 1) \)
\( y = x \)
\( y = x \) teğet doğrusunun \( f \) fonksiyonunu ikinci kez kestiği \( Q \) noktasını bulmak için iki denklemi ortak çözelim.
\( x = x^3 - 2x + 2 \)
\( x^3 - 3x + 2 = 0 \)
\( (x - 1)^2(x + 2) = 0 \)
\( x = 1 \) ya da \( x = -2 \)
\( x = 1 \) noktası \( P(1, 1) \) noktasına ait olduğuna göre doğrunun eğriyi kestiği ikinci nokta \( x = -2 \) noktasıdır.
\( x = -2 \Longrightarrow y = -2 \)
\( Q(-2, -2) \)
Fonksiyonun ve teğet doğrunun grafikleri aşağıdaki şekilde verilmiştir.

\( f(x) = ax^2 + bx + c \) fonksiyonu \( (0, -5) \) noktasından geçmektedir. Fonksiyonun \( (-1, 0) \) noktasındaki teğet doğrusunun denklemi \( y = 6 - 6x \) olduğuna göre, bu fonksiyonun kökler toplamı kaçtır?
Çözümü Göster\( (0, -5) \) noktası \( f(x) \) üzerinde olduğuna göre denklemi sağlar.
\( f(0) = -5 \)
\( a(0)^2 + b(0) + c = -5 \)
\( c = -5 \)
Aynı şekilde \( (-1, 0) \) noktası da \( f(x) \) üzerinde olduğuna göre denklemi sağlar.
\( f(-1) = 0 \)
\( a(-1)^2 + b(-1) - 5 = 0 \)
\( a - b = 5 \)
Bir fonksiyonun belirli bir noktadaki türev değeri fonksiyonun grafiğine o noktada çizilen teğetin eğimine eşittir.
\( f'(x) = 2ax + b \)
\( y = 6 - 6x \) doğrusunun eğimi \( -6 \)'dır.
\( f'(-1) = -6 \)
\( 2a(-1) + b = -6 \)
\( -2a + b = -6 \)
Bulduğumuz iki denklemi taraf tarafa toplayarak \( a \) ve \( b \) değerlerini bulalım.
\( a - b = 5 \)
\( -2a + b = -6 \)
\( -a = -1 \Longrightarrow a = 1 \)
\( 1 - b = 5 \Longrightarrow b = -4 \)
Buna göre \( f(x) \) fonksiyonu aşağıdaki gibi olur.
\( f(x) = x^2 - 4x - 5 \)
Fonksiyonun kökler toplamını bulalım.
\( x_1 + x_2 = -\dfrac{b}{a} \)
\( = -\dfrac{-4}{1} = 4 \) bulunur.
\( f(x) = ax^2 - 3x + b - 6 \) fonksiyonunun grafiğinin \( A(1, 2) \) noktasındaki teğetinin \( x \) ekseni ile pozitif yönde \( 135° \)'lik açı yapması için \( b \) kaç olmalıdır?
Çözümü GösterBir fonksiyonun birinci türevi o fonksiyonun herhangi bir noktasındaki teğetinin eğimini verir.
Fonksiyonun türevini alalım.
\( f'(x) = 2ax - 3 \)
Fonksiyonun \( A(1, 2) \) noktasındaki teğetinin eğimini bulmak için türev fonksiyonunda \( x = 1 \) koyalım.
\( f'(1) = 2a(1) - 3 = 2a - 3 \)
Bir doğrunun eğimi aynı zamanda \( x \) ekseni ile pozitif yönde yaptığı açının tanjantına eşittir.
\( 2a - 3 = \tan{135°} = -1 \)
\( a = 1 \)
Buna göre fonksiyon denklemi aşağıdaki gibi olur.
\( f(x) = x^2 - 3x + b - 6 \)
Fonksiyon \( A(1, 2) \) noktasından geçtiği için bu noktanın koordinatları \( f(x) \) denklemini sağlar.
\( f(1) = 2 \)
\( 1^2 - 3(1) + b - 6 = 2 \)
\( 1 - 3 + b - 6 = 2 \)
\( b = 10 \) bulunur.
\( y = 2x + c \) doğrusu \( f(x) = \frac{1}{3}x^3 - \frac{7}{4}x^2 - \frac{5}{2}x \) eğrisine dik olduğuna göre, \( c \)'nin alabileceği değerleri bulunuz.
Çözümü GösterBir noktadaki teğet ve normal doğruların eğimleri çarpımı \( -1 \) olur.
\( y = 2x + c \) doğrusunun eğimi 2'dir. Buna göre doğrunun eğriyi kestiği noktada teğet doğrunun eğimi \( -\frac{1}{2} \) olur.
Bir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyona o noktada teğet olan doğrunun eğimini verir.
\( f(x) = (\dfrac{1}{3}x^3 - \dfrac{7}{4}x^2 - \dfrac{5}{2}x)' \)
\( = x^2 - \dfrac{7}{2}x - \dfrac{5}{2} \)
Eğimi \( -\frac{1}{2} \) olan noktaları bulmak için birinci türevi bu değere eşitleyelim.
\( f'(x) = x^2 - \dfrac{7}{2}x - \dfrac{5}{2} = -\dfrac{1}{2} \)
\( 2x^2 - 7x - 5 = -1 \)
\( (2x + 1)(x - 4) = 0 \)
\( x \in \{-\frac{1}{2}, 4\} \)
Bu \( x \) değerlerini fonksiyonda yerine koyarak noktaların ordinat değerlerini bulalım.
\( f(-\dfrac{1}{2}) = \dfrac{1}{3}(-\dfrac{1}{2})^3 - \dfrac{7}{4}(-\dfrac{1}{2})^2 - \dfrac{5}{2}(-\dfrac{1}{2}) \)
\( = \dfrac{37}{48} \)
\( f(4) = \dfrac{1}{3}(4)^3 - \dfrac{7}{4}(4)^2 - \dfrac{5}{2}4 \)
\( = -\dfrac{50}{3} \)
Buna göre \( (-\frac{1}{2}, \frac{37}{48}) \) ve \( (4, -\frac{50}{3}) \) noktalarında eğriye çizilen teğetlerin eğimi \( -\frac{1}{2} \), bu noktalarda çizilen normallerin eğimi ise \( 2 \) olur.
Şimdi bu noktalarda çizilen ve eğimi 2 olan normal doğruların denklemlerini bulalım.
\( (-\frac{1}{2}, \frac{37}{48}) \) noktasından geçen ve eğimi 2 olan normal doğrunun denklemini bulalım.
\( y - y_1 = m(x - x_1) \)
\( y - \dfrac{37}{48} = 2(x - (-\dfrac{1}{2})) \)
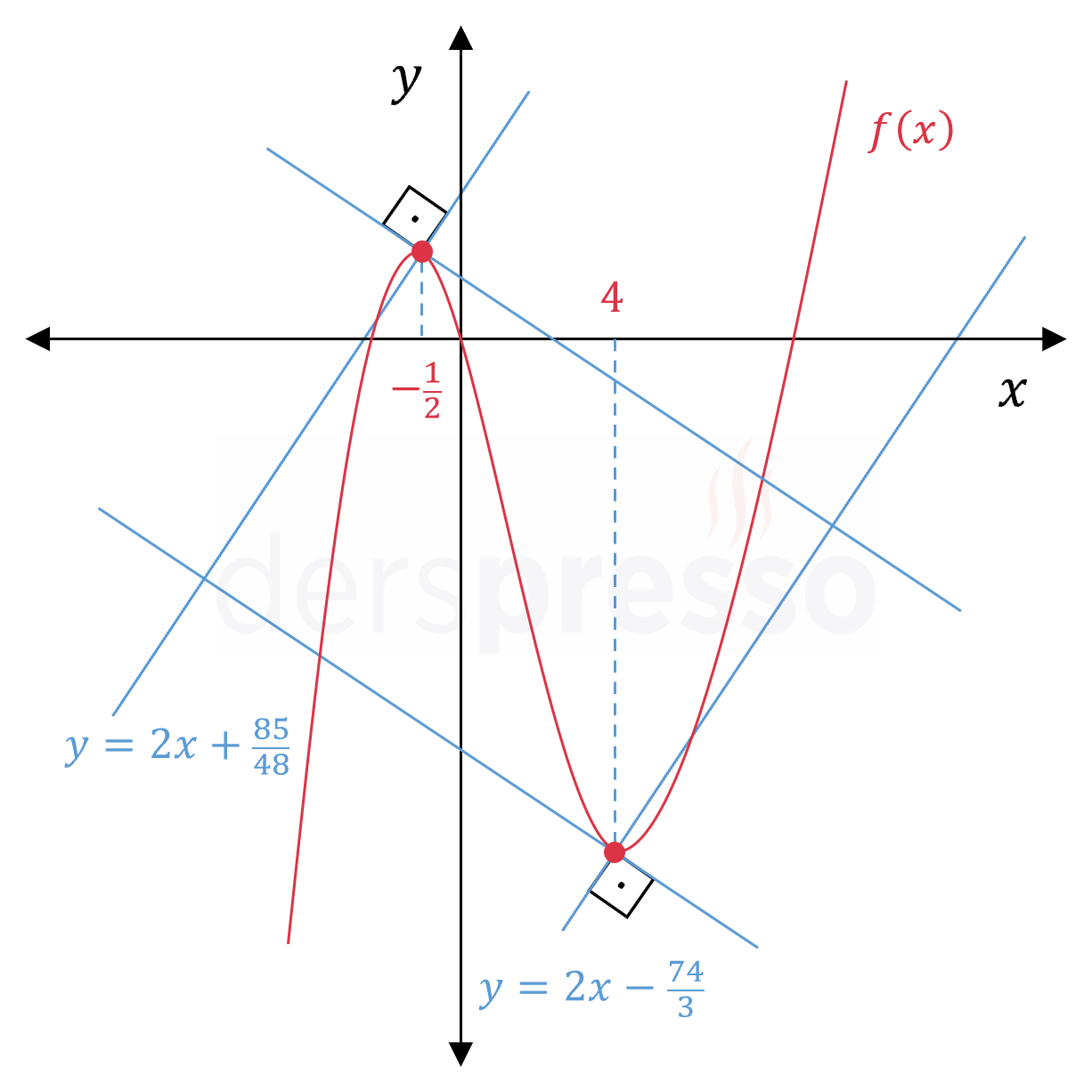
\( y = 2x + \dfrac{85}{48} \)
\( (4, -\frac{50}{3}) \) noktasından geçen ve eğimi 2 olan normal doğrunun denklemini bulalım.
\( y - (-\dfrac{50}{3}) = 2(x - 4) \)
\( y = 2x - \dfrac{74}{3} \)
Buna göre \( c \)'nin alabileceği değerler aşağıdaki gibidir.
\( c \in \{-\frac{74}{3}, \frac{85}{48}\} \)
Fonksiyonun, teğet ve normal doğruların grafikleri aşağıdaki şekilde verilmiştir.

Şekildeki \( d \) doğrusu \( y = f(x) \) eğrisine \( A(2, 4) \) noktasında teğettir.
\( g(3x) = x^2 + f(x - 2) \) ise \( g'(12) \) kaçtır?
Çözümü Göster\( y = f(x) \) eğrisi \( A(2, 4) \) noktasından geçmektedir.
\( f(2) = 4 \)
\( d \) doğrusunun eğimi \( x \) ekseni ile pozitif yönde yaptığı açının tanjantına eşittir.
\( m_d = \tan{135°} = -1 \)
\( y = f(x) \) eğrisinin \( A(2, 4) \) noktasındaki eğimi de \( -1 \) olur.
\( f'(2) = -1 \)
Verilen \( g(3x) \) fonksiyonunda iki tarafın türevini alalım.
\( g'(3x) \cdot (3x)' = 2x + f'(x - 2) \cdot (x - 2)' \)
\( 3g'(3x) = 2x + f'(x - 2) \)
Bu eşitlikte \( x = 4 \) verelim.
\( 3g'(3 \cdot 4) = 2 \cdot 4 + f'(4 - 2) \)
\( 3g'(12) = 8 + f'(2) \)
\( 3g'(12) = 8 + (-1) \)
\( g'(12) = \dfrac{7}{3} \) bulunur.
\( f(x) = \cos(3x) \) olarak veriliyor.
Buna göre \( [0, 2\pi] \) aralığında \( f'(x) + f'''(x) = 16 \) eşitliği kaç farklı değer için sağlanır?
Çözümü GösterSoruda istenen fonksiyonları bulmak için arka arkaya türev alalım.
\( f'(x) = -3\sin(3x) \)
\( f''(x) = -9\cos(3x) \)
\( f'''(x) = 27\sin(3x) \)
Fonksiyonları verilen eşitlikte yerine koyalım.
\( -3\sin(3x) + 27\sin(3x) = 16 \)
\( 24\sin(3x) = 16 \)
\( \sin(3x) = \dfrac{2}{3} \)
\( \sin(3x) \) fonksiyonunun grafiğini çizelim.
\( \sin(3x) \) fonksiyonunun periyodu \( \frac{2\pi}{3} \) olur.
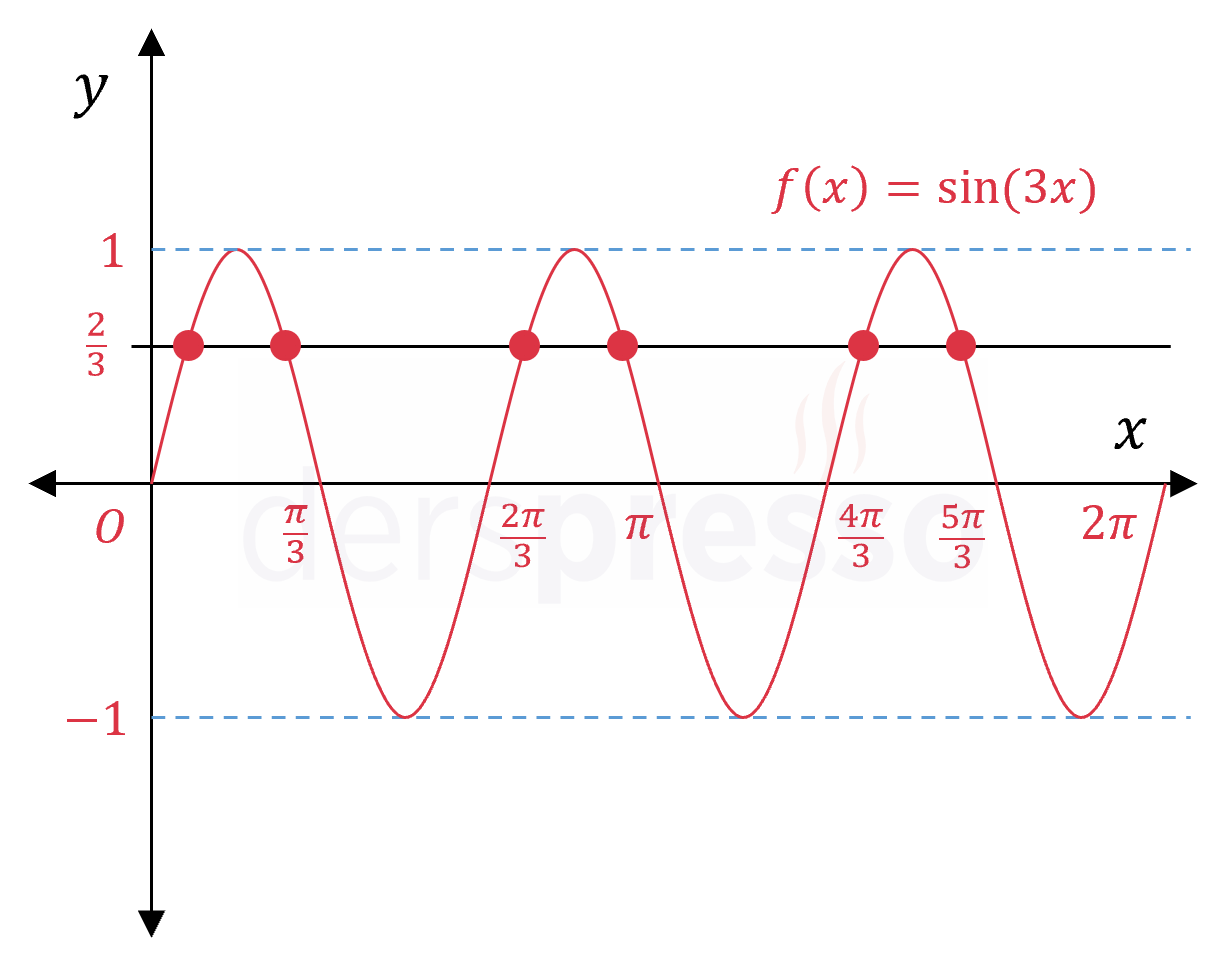
\( y = \dfrac{2}{3} \) doğrusu grafiği 6 noktada kestiğine göre eşitlik 6 farklı değer için sağlanır.