Lineerleştirme
Lineerleştirme, bir fonksiyona türevli olduğu bir \( x = a \) noktasında teğet olan doğruyu kullanarak bu noktaya yakın noktalardaki yaklaşık fonksiyon değerini hesaplamamızı sağlayan bir yaklaşım yöntemidir. Bu yöntemin bir diğer adı lineer yaklaşımdır.
Bir \( f \) fonksiyonuna türevli olduğu bir \( x = a \) noktasında teğet olan doğrunun denklemi aşağıdaki formülle bulunur.
\( L(x) = f(a) + f'(a)(x - a) \)
İSPATI GÖSTER
\( f \) fonksiyonunun \( x = a \) apsisli noktadaki koordinatları \( (a, f(a)) \) olur.
Fonksiyona bu noktada teğet olan doğrunun eğimi, fonksiyonun birinci türevinin bu noktadaki değeri, yani \( m = f'(a) \) olur.
Bir noktası \( (x_1, y_1) = (a, f(a)) \) ve eğimi \( m = f'(a) \) olan doğrunun denklemini yazalım.
\( y - y_1 = m(x - x_1) \)
\( y - f(a) = f'(a)(x - a) \)
Buna göre \( f \) fonksiyonunun türevli olduğu \( x = a \) noktasındaki teğet doğru denklemi aşağıdaki gibidir.
\( L(x) = y = f(a) + f'(a)(x - a) \)
Örnek olarak \( f(x) = 2x^3 \) fonksiyonuna \( x = 1 \) noktasında teğet olan \( L(x) \) doğrusunun denklemini bulalım.
\( f(x) = 2x^3 \)
Fonksiyona \( a = 1 \) apsisli noktada teğet olan doğrunun denklemi:
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(1) + f'(1)(x - 1) \)
\( f(1) = 2(1)^3 = 2 \)
\( f'(x) = 6x^2 \)
\( f'(1) = 6(1)^2 = 6 \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = 2 + 6(x - 1) = 6x - 4 \)
Fonksiyonun ve \( x = 1 \) apsisli noktadaki teğetinin grafiği aşağıdaki gibidir.
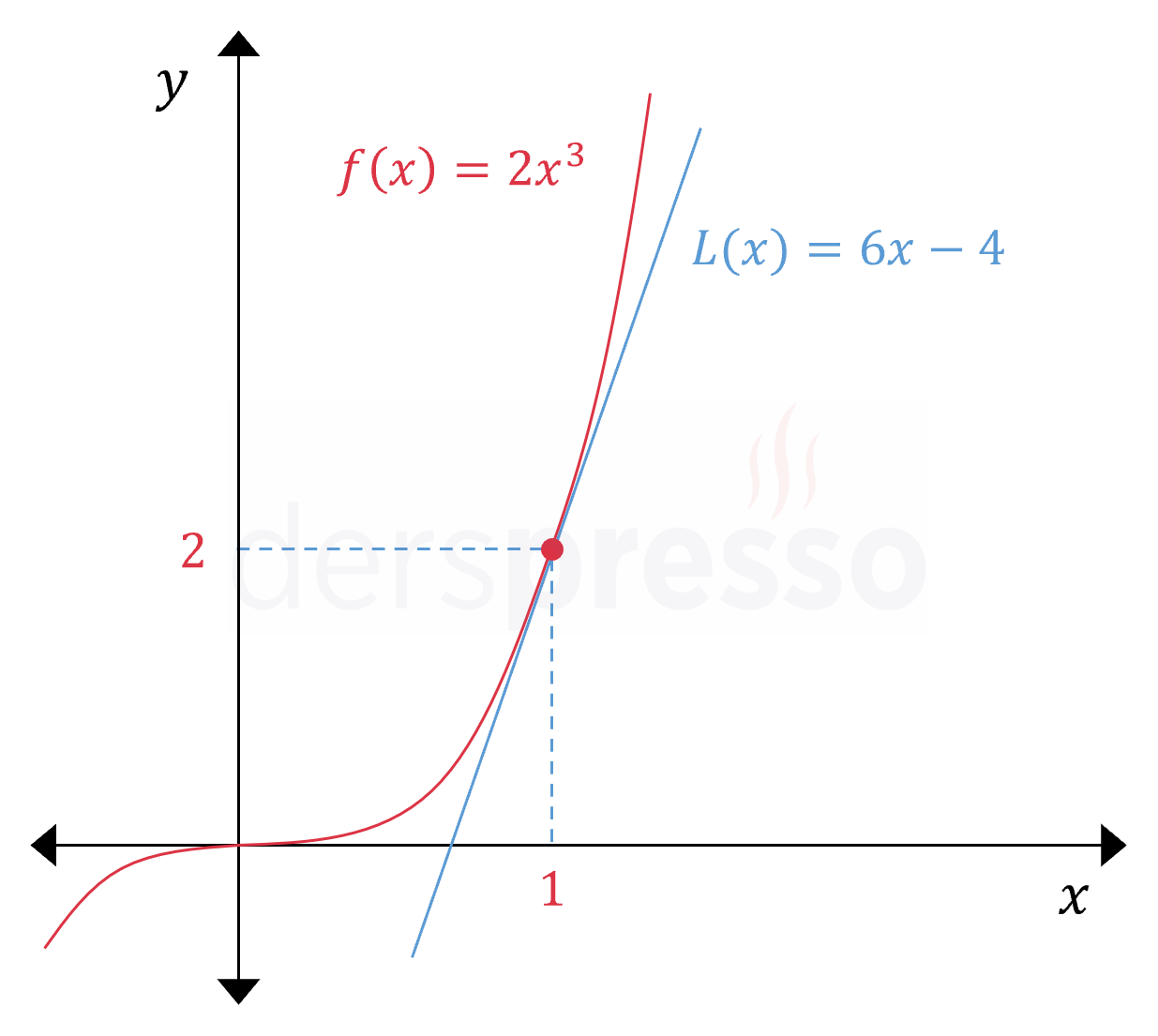
Fonksiyonun \( (1, 2) \) noktası civarındaki grafiğini yakından incelediğimizde; teğet doğrunun bu noktaya yakın noktalarda fonksiyona oldukça yakın değerler aldığını, bu noktadan uzaklaştıkça da doğrunun ve fonksiyonun aldığı değerlerin farklılaştığını görürüz.
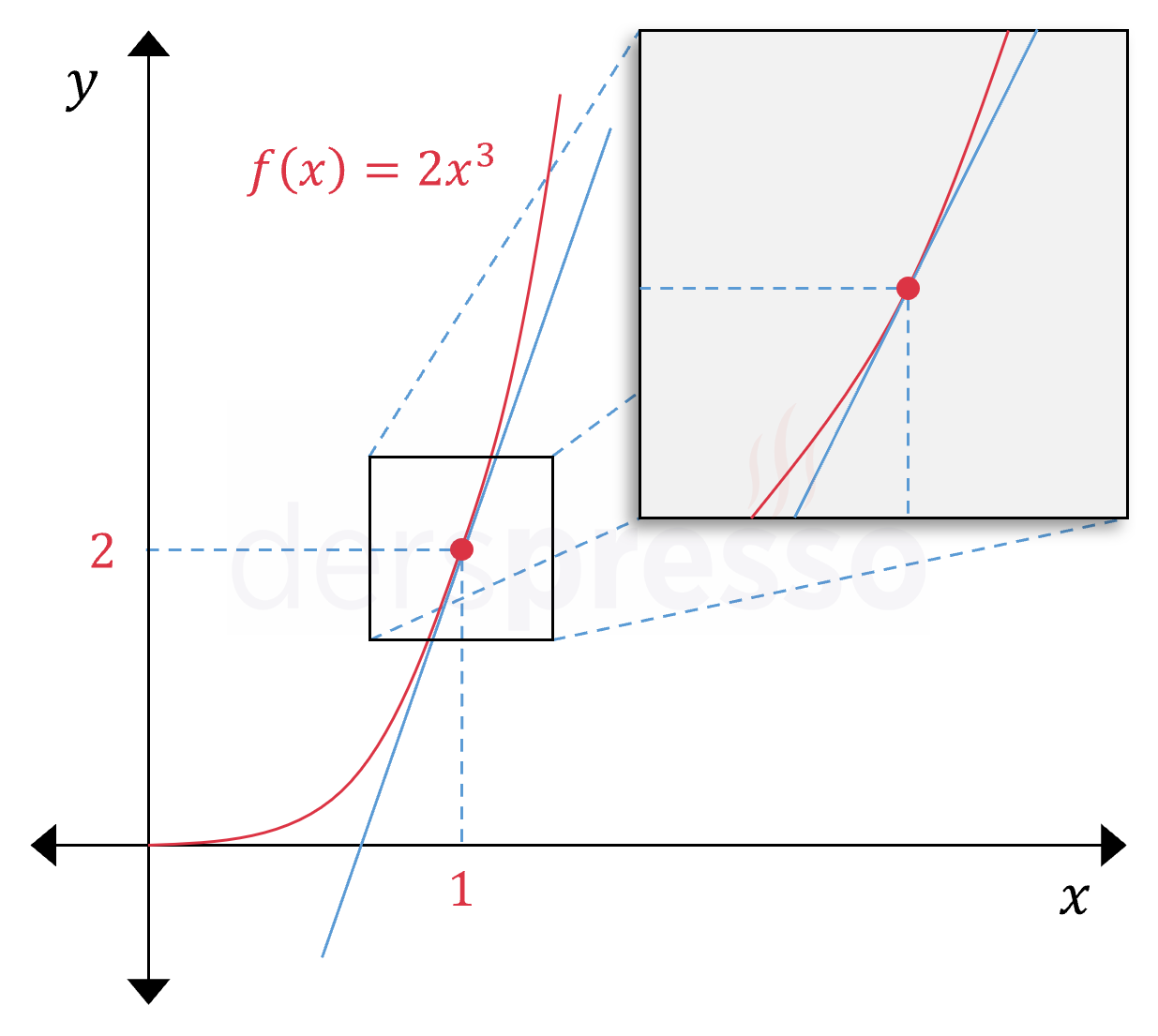
Bunu sayısal olarak teyit etmek için, \( x = 1 \) noktasına yakın birkaç noktada fonksiyonun ve teğet doğrunun aldığı değerleri karşılaştıralım. Aşağıdaki grafikte ve tabloda fonksiyonun aldığı değerler \( f(x) \), teğet doğrunun aldığı değerler \( L(x) \) ile gösterilmiştir.
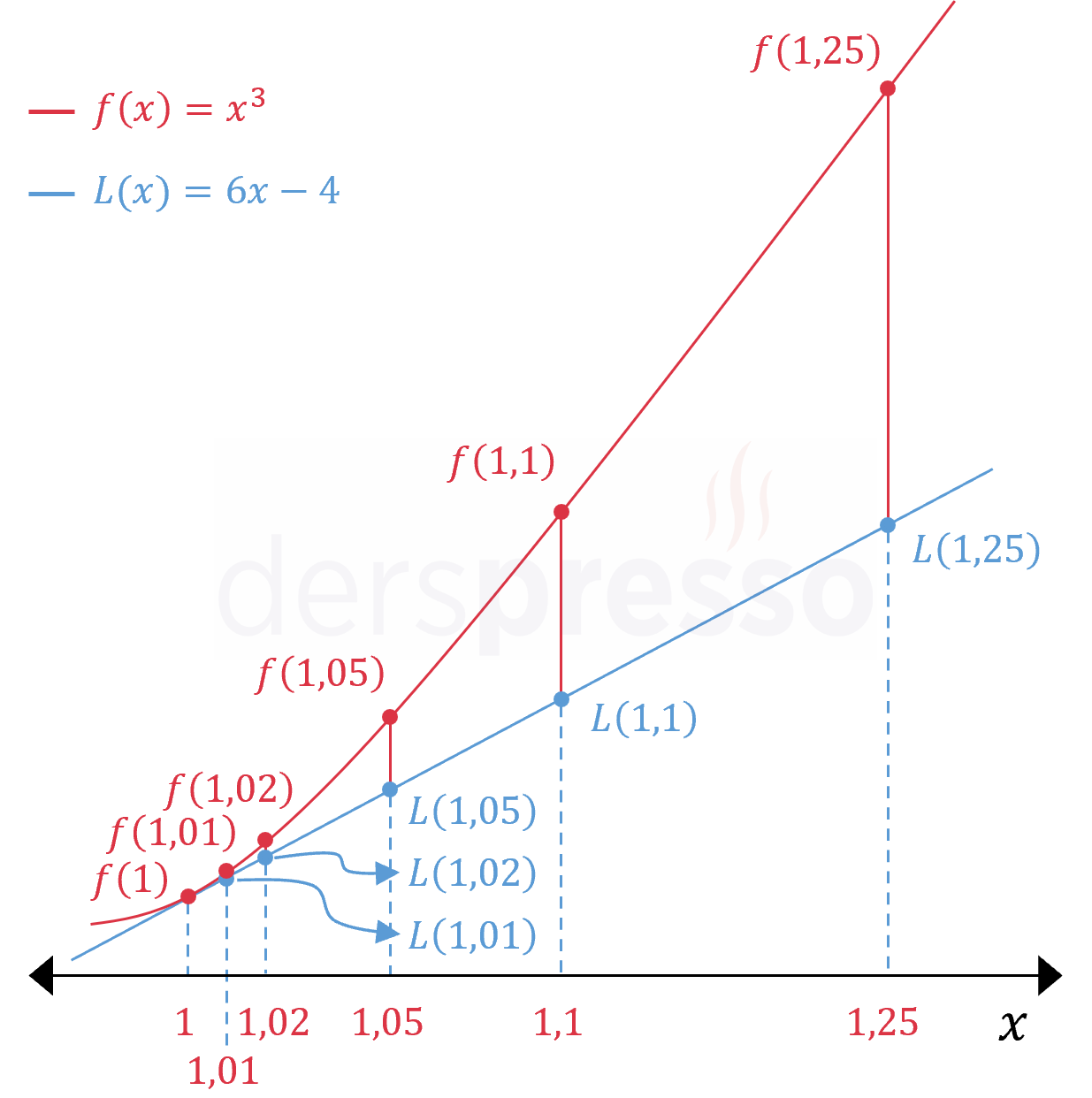
| \( x \) | \( L(x) \) | \( f(x) \) | \( \abs{f(x) - L(x)} \) |
|---|---|---|---|
| \( 1 \) | \( 3(1) - 2 = 1 \) | \( 1^3 = 1 \) | \( 0 \) |
| \( 1,01 \) | \( 3(1,01) - 2 = 1,03 \) | \( 1,01^3 = 1,030301 \) | \( 0,000301 \) |
| \( 1,02 \) | \( 3(1,02) - 2 = 1,06 \) | \( 1,02^3 = 1,061208 \) | \( 0,001208 \) |
| \( 1,05 \) | \( 3(1,05) - 2 = 1,15 \) | \( 1,05^3 = 1,157625 \) | \( 0,007625 \) |
| \( 1,1 \) | \( 3(1,1) - 2 = 1,3 \) | \( 1,1^3 = 1,331 \) | \( 0,031 \) |
| \( 1,25 \) | \( 3(1,25) - 2 = 1,75 \) | \( 1,25^3 = 1,953125 \) | \( 0,203125 \) |
| \( 1,5 \) | \( 3(1,5) - 2 = 2,5 \) | \( 1,5^3 = 3,375 \) | \( 0,875 \) |
| \( 1,75 \) | \( 3(1,75) - 2 = 3,25 \) | \( 1,75^3 = 5,359375 \) | \( 2,109375 \) |
| \( 2 \) | \( 3(2) - 2 = 4 \) | \( 2^3 = 8 \) | \( 4 \) |
Hem grafikte hem de tabloda görebileceğimiz üzere; bir fonksiyona belirli bir \( x = a \) noktasında teğet olan doğru, bu noktaya yakın noktalarda fonksiyonun gerçek değerine oldukça yakın değerlere sahiptir, dolayısıyla fonksiyonun gerçek değerini hesaplamanın çok işlem gerektirdiği ve yaklaşık bir değerin yeterli olduğu durumlarda fonksiyon yerine bu teğet doğrunun denklemi kullanılabilir.
\( x \) noktası \( a \)'ya yakın bir nokta olmak üzere,
\( L(x) \approx f(x) \)
Lineerleştirme yöntemini bir örnek üzerinde gösterelim.
\( \sqrt{16,1} \) ifadesinin yaklaşık değerini bulalım.
İfadenin yaklaşık değerini bulmak için karekök fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \sqrt{x} \)
\( x = 16,1 \) noktasına en yakın ve karekökünü kolaylıkla hesaplayabileceğimiz değer \( x = 16 \) değeridir.
Fonksiyona \( a = 16 \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(16) + f'(16)(x - 16) \)
\( f(16) = \sqrt{16} = 4 \)
\( f'(x) = \dfrac{1}{2\sqrt{x}} \)
\( f'(16) = \dfrac{1}{2\sqrt{16}} = \dfrac{1}{8} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(16) + f'(16)(x - 16) \)
\( = 4 + \dfrac{1}{8}(x - 16) \)
\( = \dfrac{1}{8}x + 2 \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = 16 \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(16,1) = \dfrac{1}{8}16,1 + 2 = 4,0125 \)
Verilen ifadenin gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(16,1) = \sqrt{16,1} = 4,0124805\ldots \)
\( L(16,1) \approx f(16,1) \)
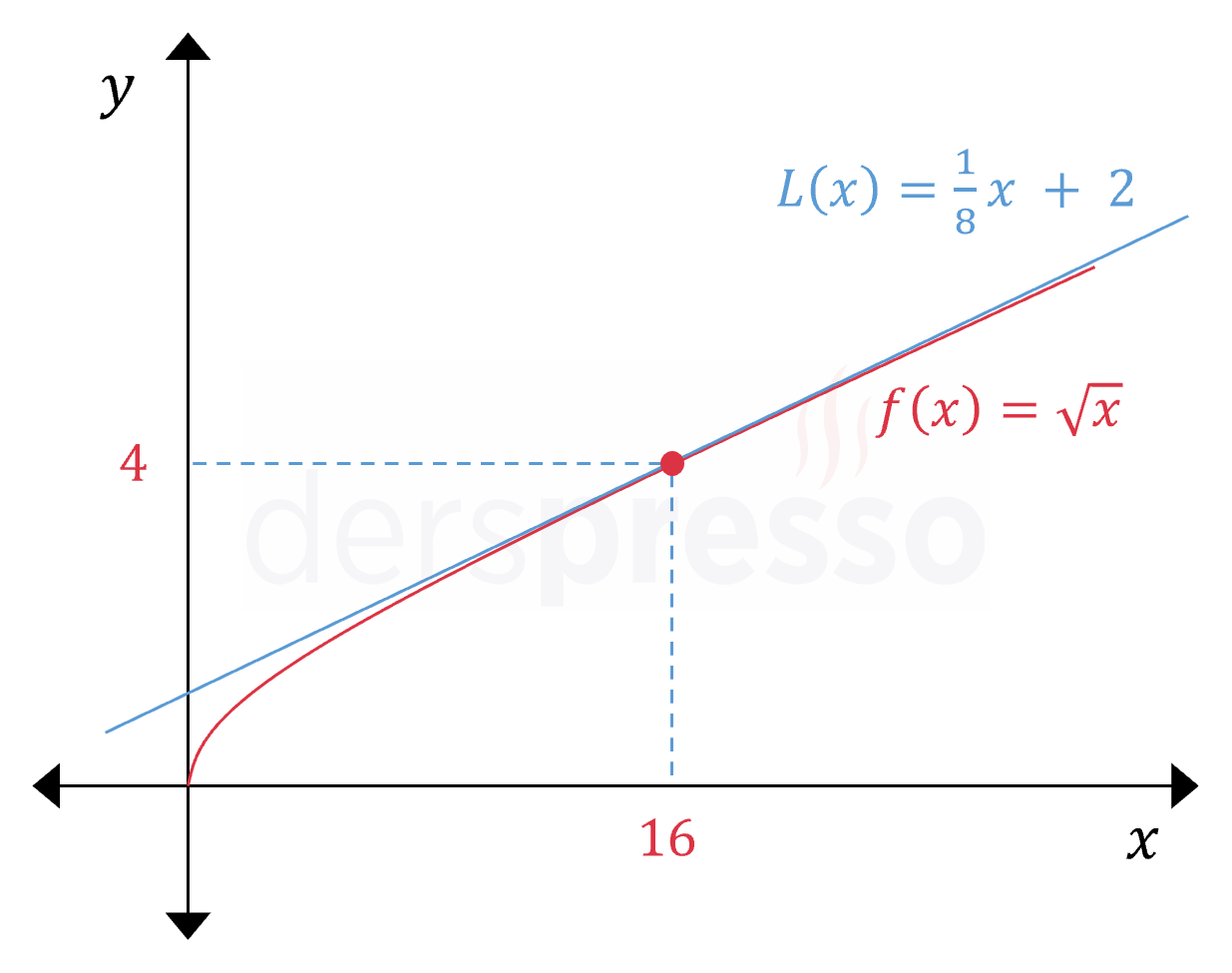
Aşağıda \( f \) fonksiyonun ve \( x = 16 \) noktasındaki teğetinin grafikleri verilmiştir.
Aşağıdaki fonksiyonlara belirtilen \( x \) değerlerinde teğet olan doğruların denklemini bulunuz.
(a) \( f(x) = 2x^3 + 3x^2 - 6, \quad x = \dfrac{1}{2} \)
(b) \( g(x) = \dfrac{1}{2}x^4 - 5x^2, \quad x = 2 \)
(c) \( h(x) = x^{\frac{5}{4}} + \dfrac{1}{2}x^{\frac{1}{2}}, \quad x = 16 \)
Çözümü GösterBir \( f \) fonksiyonuna \( x = a \) noktasında teğet olan doğrunun denklemi aşağıdaki formülle bulunur.
\( L(x) = f(a) + f'(a)(x - a) \)
(a) seçeneği:
\( f(x) = 2x^3 + 3x^2 - 6 \)
Fonksiyona \( x = \frac{1}{2} \) noktasında teğet olan doğrunun denklemi:
\( L(x) = f(\dfrac{1}{2}) + f'(\dfrac{1}{2})(x - \dfrac{1}{2}) \)
\( f(\dfrac{1}{2}) = 2(\dfrac{1}{2})^3 + 3(\dfrac{1}{2})^2 - 6 = - 5 \)
\( f'(x) = 6x^2 + 6x \)
\( f'(\dfrac{1}{2}) = 6(\dfrac{1}{2})^2 + 6(\dfrac{1}{2}) = \dfrac{9}{2} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = -5 + \dfrac{9}{2}(x - \dfrac{1}{2}) \)
\( = \dfrac{9}{2}x - \dfrac{29}{4} \)
(b) seçeneği:
\( g(x) = \dfrac{1}{2}x^4 - 5x^2 \)
Fonksiyona \( x = 2 \) noktasında teğet olan doğrunun denklemi:
\( L(x) = g(2) + g'(2)(x - 2) \)
\( g(2) = \dfrac{1}{2}(2)^4 - 5(2)^2 = -12 \)
\( g'(x) = 2x^3 - 10x \)
\( g'(2) = 2(2)^3 - 10(2) = -4 \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = -12 + (-4)(x - 2) \)
\( = -4x - 4 \)
(c) seçeneği:
\( h(x) = x^{\frac{5}{4}} + \dfrac{1}{2}x^{\frac{1}{2}} \)
Fonksiyona \( x = 16 \) noktasında teğet olan doğrunun denklemi:
\( L(x) = h(16) + h'(16)(x - 16) \)
\( h(16) = 16^{\frac{5}{4}} + \dfrac{1}{2}(16)^{\frac{1}{2}} \)
\( = 32 + 2 = 34 \)
\( h'(x) = \dfrac{5}{4}x^{\frac{1}{4}} + \dfrac{1}{4}x^{-\frac{1}{2}} \)
\( h'(16) = \dfrac{5}{4}16^{\frac{1}{4}} + \dfrac{1}{4}16^{-\frac{1}{2}} \)
\( = \dfrac{5}{2} + \dfrac{1}{16} = \dfrac{41}{16} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = 34 + \dfrac{41}{16}(x - 16) \)
\( = \dfrac{41}{16}x - 7 \)
\( \sqrt{47} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için karekök fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \sqrt{x} \)
\( x = 47 \) noktasına en yakın ve karekökünü kolaylıkla hesaplayabileceğimiz değer \( x = 49 \) değeridir.
Fonksiyona \( a = 49 \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(49) + f'(49)(x − 49) \)
\( f(49) = \sqrt{49} = 7 \)
\( f'(x) = \dfrac{1}{2\sqrt{x}} \)
\( f'(49) = \dfrac{1}{2\sqrt{49}} = \dfrac{1}{14} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(49) + f'(49)(x − 49) \)
\( = 7 + \dfrac{1}{14}(x - 49) \)
\( = \dfrac{1}{14}x + \dfrac{7}{2} \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = 49 \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(47) = \dfrac{1}{14}47 + \dfrac{7}{2} = 6,8571\ldots \)
Fonksiyonun \( x = 47 \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(47) = \sqrt{47} = 6,8556\ldots \)
\( L(47) \approx f(47) \)
\( \sqrt[4]{0,0079} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için 4. mertebeden kök fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \sqrt[4]{x} \)
\( x = 0,0079 \) noktasına en yakın ve 4. mertebeden kökünü kolaylıkla hesaplayabileceğimiz değer \( x = 0,0081 \) değeridir.
Fonksiyona \( a = 0,0081 \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(0,0081) + f'(0,0081)(x − 0,0081) \)
\( f(0,0081) = \sqrt[4]{0,0081} = \sqrt[4]{(0,3)^4} = 0,3 \)
\( f'(x) = \dfrac{1}{4\sqrt[4]{x^3}} \)
\( f'(0,0081) = \dfrac{1}{4\sqrt[4]{(0,0081)^3}} \)
\( = \dfrac{1}{4(0,3)^3} = \dfrac{1}{0,108} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(0,0081) + f'(0,0081)(x - 0,0081) \)
\( = 0,3 + \dfrac{1}{0,108}(x - 0,0081) \)
\( = \dfrac{1}{0,108}x + 0,225 \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = 0,0081 \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(0,0079) = \dfrac{1}{0,108}0,0079 + 0,225 = 0,298148\ldots \)
Fonksiyonun \( x = 0,0079 \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(0,0079) = \sqrt[4]{0,0079} = 0,298130\ldots \)
\( L(0,0079) \approx f(0,0079) \)
\( \sqrt[3]{(122,5)^2} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için küp kök fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \sqrt[3]{x^2} \)
\( x = 122,5 \) noktasına en yakın ve küp kökünü kolaylıkla hesaplayabileceğimiz değer \( x = 125 \) değeridir.
Fonksiyona \( a = 125 \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(125) + f'(125)(x − 125) \)
\( f(125) = \sqrt[3]{125^2} = 25 \)
\( f'(x) = \dfrac{2}{3\sqrt[3]{x}} \)
\( f'(125) = \dfrac{2}{3\sqrt[3]{125}} = \dfrac{2}{15} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(125) + f'(125)(x - 125) \)
\( = 25 + \dfrac{2}{15}(x - 125) \)
\( = \dfrac{2}{15}x + \dfrac{25}{3} \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = 125 \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(122,5) = \dfrac{2}{15}(122,5) + \dfrac{25}{3} = 24,6666\ldots \)
Fonksiyonun \( x = 122,5 \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(122,5) = \sqrt[3]{(122,5)^2} = 24,6655\ldots \)
\( L(122,5) \approx f(122,5) \)
\( f(x) = \sqrt{x} + \sqrt[3]{x} \) fonksiyonunun \( x = 61 \) noktasındaki yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için fonksiyona lineerleştirme yöntemini uygulayalım.
\( f(x) = \sqrt{x} + \sqrt[3]{x} \)
\( x = 61 \) noktasına en yakın ve hem karekök hem küp kök değerini kolaylıkla hesaplayabileceğimiz değer \( x = 64 \) değeridir.
Fonksiyona \( a = 64 \) apsisli noktada teğet olan doğrunun denklemi:
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(64) + f'(64)(x − 64) \)
\( f(64) = \sqrt{64} + \sqrt[3]{64} = 8 + 4 = 12 \)
\( f'(x) = \dfrac{1}{2\sqrt{x}} + \dfrac{1}{3\sqrt[3]{x^2}} \)
\( f'(64) = \dfrac{1}{2\sqrt{64}} + \dfrac{1}{3\sqrt[3]{64^2}} \)
\( = \dfrac{1}{16} + \dfrac{1}{48} = \dfrac{1}{12} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(64) + f'(64)(x − 64) \)
\( = 12 + \dfrac{1}{12}(x - 64) \)
\( = \dfrac{1}{12}x + \dfrac{20}{3} \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = 64 \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(61) = \dfrac{1}{12}61 + \dfrac{20}{3} = 11,75 \)
Fonksiyonun \( x = 61 \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(61) = 11,7467\ldots \)
\( L(61) \approx f(61) \)
\( \ln{3} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için doğal logaritma fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \ln{x} \)
\( x = 3 \) noktasına en yakın ve doğal logaritmasını kolaylıkla hesaplayabileceğimiz değer \( x = e = 2,7182\ldots \) değeridir.
Fonksiyona \( a = e \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(e) + f'(e)(x − e) \)
\( f(e) = \ln{e} = 1 \)
\( f'(x) = \dfrac{1}{x} \)
\( f'(e) = \dfrac{1}{e} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(e) + f'(e)(x - e) \)
\( = 1 + \dfrac{1}{e}(x - e) \)
\( = \dfrac{1}{e}x \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = e \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(3) = \dfrac{1}{e}3 = 1,1036\ldots \)
Fonksiyonun \( x = 3 \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(3) = \ln{3} = 1,0986\ldots \)
\( L(3) \approx f(3) \)
\( f(x) = x^3 - 6x^2 + 7x + 2 \) fonksiyonunun \( x = 1,092 \) noktasındaki yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için polinom fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = x^3 - 6x^2 + 7x + 2 \)
\( x = 1,092 \) noktasına en yakın ve fonksiyon değerini kolaylıkla hesaplayabileceğimiz değer \( x = 1 \) değeridir.
Fonksiyona \( a = 1 \) apsisli noktada teğet olan doğrunun denklemi:
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(1) + f'(1)(x − 1) \)
\( f(1) = 1^3 - 6(1)^2 + 7(1) + 2 = 4 \)
\( f'(x) = 3x^2 - 12x + 7 \)
\( f'(1) = 3(1)^2 - 12(1) + 7 = -2 \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(1) + f'(1)(x − 1) \)
\( = 4 + (-2)(x - 1) \)
\( = -2x + 6 \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = 1 \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(1,092) = -2(1,092) + 6 = 3,816 \)
Fonksiyonun \( x = 1,092 \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(1,092) = 3,7913\ldots \)
\( L(1,092) \approx f(1,092) \)
\( f(x) = \dfrac{7}{27}\sqrt{(x + 9)^3} \) fonksiyonunun \( x = 0,165 \) noktasındaki yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için karekök fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \dfrac{7}{27}\sqrt{(x + 9)^3} \)
\( x = 0,165 \) noktasına en yakın ve karekökünü kolaylıkla hesaplayabileceğimiz değer \( x = 0 \) değeridir.
Fonksiyona \( a = 0 \) apsisli noktada teğet olan doğrunun denklemi:
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(0) + f'(0)(x − 0) \)
\( f(0) = \dfrac{7}{27}\sqrt{(0 + 9)^3} = 7 \)
\( f'(x) = \dfrac{7}{18}\sqrt{x + 9} \)
\( f'(0) = \dfrac{7}{18}\sqrt{0 + 9} = \dfrac{7}{6} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(0) + f'(0)(x − 0) \)
\( = 7 + \dfrac{7}{6}(x - 0) \)
\( = \dfrac{7}{6}x + 7 \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = 0 \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(0,165) = \dfrac{7}{6}(0,165) + 7 = 7,1925 \)
Fonksiyonun \( x = 0,165 \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz
\( f(0,165) = 7,1933\ldots \)
\( L(0,165) \approx f(0,165) \)
\( \sqrt{96,5} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için karekök fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \sqrt{x} \)
\( x = 96,5 \) noktasına en yakın ve karekökünü kolaylıkla hesaplayabileceğimiz değer \( x = 100 \) değeridir.
Fonksiyona \( a = 100 \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(100) + f'(100)(x − 100) \)
\( f(100) = \sqrt{100} = 10 \)
\( f'(x) = \dfrac{1}{2\sqrt{x}} \)
\( f'(100) = \dfrac{1}{2\sqrt{100}} = \dfrac{1}{20} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(100) + f'(100)(x - 100) \)
\( = 10 + \dfrac{1}{20}(x - 100) \)
\( = \dfrac{1}{20}x + 5 \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = 100 \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(96,5) = \dfrac{1}{20}96,5 + 5 = 9,825 \)
Fonksiyonun \( x = 96,5 \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(96,5) = \sqrt{96,5} = 9,8234\ldots \)
\( L(96,5) \approx f(96,5) \)
\( \sqrt[3]{\dfrac{23}{64}} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için küp kök fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \sqrt[3]{x} \)
\( x = \frac{23}{64} \) noktasına en yakın ve küp kökünü kolaylıkla hesaplayabileceğimiz değer \( x = \frac{27}{64} \) değeridir.
Fonksiyona \( a = \frac{27}{64} \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(\dfrac{27}{64}) + f'(\dfrac{27}{64})(x − \dfrac{27}{64}) \)
\( f(\dfrac{27}{64}) = \sqrt[3]{\dfrac{27}{64}} = \dfrac{3}{4} \)
\( f'(x) = \dfrac{1}{3\sqrt[3]{x^2}} \)
\( f'(\dfrac{27}{64}) = \dfrac{1}{3\sqrt[3]{(\frac{27}{64})^2}} \)
\( = \dfrac{1}{3(\frac{9}{16})} = \dfrac{16}{27} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(\dfrac{27}{64}) + f'(\dfrac{27}{64})(x - \dfrac{27}{64}) \)
\( = \dfrac{3}{4} + \dfrac{16}{27}(x - \dfrac{27}{64}) \)
\( = \dfrac{16}{27}x + \dfrac{1}{2} \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = \frac{27}{64} \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(\dfrac{23}{64}) = \dfrac{16}{27}(\dfrac{23}{64}) + \dfrac{1}{2} = 0,7129\ldots \)
Fonksiyonun \( x = \frac{23}{64} \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(\dfrac{23}{64}) = \sqrt[3]{\dfrac{23}{64}} = 0,7109\ldots \)
\( L(\dfrac{23}{64}) \approx f(\dfrac{23}{64}) \)
\( \dfrac{1}{\sqrt[5]{28}} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için 5. dereceden kök fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \dfrac{1}{\sqrt[5]{x}} \)
\( x = 28 \) noktasına en yakın ve 5. dereceden kökünü kolaylıkla hesaplayabileceğimiz değer \( x = 32 \) değeridir.
Fonksiyona \( a = 32 \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(32) + f'(32)(x − 32) \)
\( f(32) = \dfrac{1}{\sqrt[5]{32}} = \dfrac{1}{2} \)
\( f'(x) = -\dfrac{1}{5\sqrt[5]{x^6}} \)
\( f'(32) = -\dfrac{1}{5\sqrt[5]{32^6}} = -\dfrac{1}{320} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(32) + f'(32)(x - 32) \)
\( = \dfrac{1}{2} + (-\dfrac{1}{320})(x - 32) \)
\( = -\dfrac{1}{320}x + \dfrac{3}{5} \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = 32 \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(28) = -\dfrac{1}{320}28 + \dfrac{3}{5} = 0,5125 \)
Fonksiyonun \( x = 28 \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(28) = \dfrac{1}{\sqrt[5]{28}} = 0,5135\ldots \)
\( L(28) \approx f(28) \)
\( \sin{58°} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için sinüs fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \sin{x} \)
\( x = 58° \) değerine en yakın ve sinüsünü kolaylıkla hesaplayabileceğimiz değer \( x = 60° = \frac{\pi}{3} \) değeridir.
Fonksiyona \( a = \frac{\pi}{3} \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(\dfrac{\pi}{3}) + f'(\dfrac{\pi}{3})(x - \dfrac{\pi}{3}) \)
\( f(\dfrac{\pi}{3}) = \sin{\dfrac{\pi}{3}} = \dfrac{\sqrt{3}}{2} \)
\( f'(x) = \cos{x} \)
\( f'(\dfrac{\pi}{3}) = \cos{\dfrac{\pi}{3}} = \dfrac{1}{2} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(\dfrac{\pi}{3}) + f'(\dfrac{\pi}{3})(x - \dfrac{\pi}{3}) \)
\( = \dfrac{\sqrt{3}}{2} + \dfrac{1}{2}(x - \dfrac{\pi}{3}) \)
\( = \dfrac{1}{2}x + \dfrac{\sqrt{3}}{2} - \dfrac{\pi}{6} \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = \frac{\pi}{3} \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( x = 58° \) için \( L(x) \) değerini hesaplamak için açı ölçüsünü önce radyana çevirelim.
Derece cinsinden verilen bir açıyı radyana çevirmek için açı \( \frac{\pi}{180°} \) ile çarpılır.
\( 58° = 58° \cdot \dfrac{\pi}{180°} = \dfrac{29\pi}{90} \) radyan
\( L(58°) = L(\dfrac{29\pi}{90}) = \dfrac{1}{2} \cdot \dfrac{29\pi}{90} + \dfrac{\sqrt{3}}{2} - \dfrac{\pi}{6} \)
\( = \dfrac{\sqrt{3}}{2} - \dfrac{\pi}{180} = 0,8485\ldots \)
Fonksiyonun \( x = 58° \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(58°) = \sin{58°} = 0,8480\ldots \)
\( L(58°) \approx f(58°) \)
\( \cos{32°} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için kosinüs fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \cos{x} \)
\( x = 32° \) değerine en yakın ve kosinüsünü kolaylıkla hesaplayabileceğimiz değer \( x = 30° = \frac{\pi}{6} \) değeridir.
Fonksiyona \( a = \frac{\pi}{6} \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(\dfrac{\pi}{6}) + f'(\dfrac{\pi}{6})(x − \dfrac{\pi}{6}) \)
\( f(\dfrac{\pi}{6}) = \cos{\dfrac{\pi}{6}} = \dfrac{\sqrt{3}}{2} \)
\( f'(x) = -\sin{x} \)
\( f'(\dfrac{\pi}{6}) = -\sin{\dfrac{\pi}{6}} = -\dfrac{1}{2} \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(\dfrac{\pi}{6}) + f'(\dfrac{\pi}{6})(x - \dfrac{\pi}{6}) \)
\( = \dfrac{\sqrt{3}}{2} + (-\dfrac{1}{2})(x - \dfrac{\pi}{6}) \)
\( = -\dfrac{1}{2}x + \dfrac{\sqrt{3}}{2} + \dfrac{\pi}{12} \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = \frac{\pi}{6} \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( x = 32° \) için \( L(x) \) değerini hesaplamak için açı ölçüsünü önce radyana çevirelim.
Derece cinsinden verilen bir açıyı radyana çevirmek için açı \( \frac{\pi}{180°} \) ile çarpılır.
\( 32° = 32° \cdot \dfrac{\pi}{180} = \dfrac{8\pi}{45} \)
\( L(32°) = L(\dfrac{8\pi}{45}) = \dfrac{\sqrt{3}}{2} - \dfrac{\frac{8\pi}{45}}{2} + \dfrac{\pi}{12} \)
\( = \dfrac{\sqrt{3}}{2} - \dfrac{\pi}{180} = 0,8485\ldots \)
Fonksiyonun \( x = 32° \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(32°) = \cos{32°} = 0,8480\ldots \)
\( L(32°) \approx f(32°) \)
\( \tan{41°} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için tanjant fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = \tan{x} \)
\( x = 41° \) değerine en yakın ve kosinüsünü kolaylıkla hesaplayabileceğimiz değer \( x = 45° = \frac{\pi}{4} \) değeridir.
Fonksiyona \( a = \frac{\pi}{4} \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(\dfrac{\pi}{4}) + f'(\dfrac{\pi}{4})(x − \dfrac{\pi}{4}) \)
\( f(\dfrac{\pi}{4}) = \tan{\dfrac{\pi}{4}} = 1 \)
\( f'(x) = 1 + \tan^2{x} \)
\( f'(\dfrac{\pi}{4}) = 1 + \tan^2{\dfrac{\pi}{4}} = 1 + 1^2 = 2 \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(\dfrac{\pi}{4}) + f'(\dfrac{\pi}{4})(x - \dfrac{\pi}{4}) \)
\( = 1 + 2(x - \dfrac{\pi}{4}) \)
\( = 2x + 1 - \dfrac{\pi}{2} \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = \frac{\pi}{4} \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( x = 41° \) için \( L(x) \) değerini hesaplamak için açı ölçüsünü önce radyana çevirelim.
Derece cinsinden verilen bir açıyı radyana çevirmek için açı \( \frac{\pi}{180°} \) ile çarpılır.
\( 41° = 41° \cdot \dfrac{\pi}{180} = \dfrac{41\pi}{180} \)
\( L(41°) = L(\dfrac{41\pi}{180}) = 2(\dfrac{41\pi}{180}) + 1 - \dfrac{\pi}{2} \)
\( = 1 - \dfrac{2\pi}{45} = 0,8603\ldots \)
Fonksiyonun \( x = 41° \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(41°) = \tan{41°} = 0,8692\ldots \)
\( L(41°) \approx f(41°) \)
\( f(x) = x\ln{x} + \sqrt{6x + 3} \) fonksiyonunun \( x = 1,245 \) noktasındaki yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için fonksiyona lineerleştirme yöntemini uygulayalım.
\( x = 1,245 \) noktasına en yakın ve fonksiyon değerini kolaylıkla hesaplayabileceğimiz değer \( x = 1 \) değeridir.
Fonksiyona \( a = 1 \) apsisli noktada teğet olan doğrunun denklemi:
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(1) + f'(1)(x − 1) \)
\( f(1) = (1)\ln{1} + \sqrt{6(1) + 3} = 3 \)
\( f'(x) = \ln{x} + 1 + \dfrac{3}{\sqrt{6x + 3}} \)
\( f'(1) = \ln{1} + 1 + \dfrac{3}{\sqrt{6(1) + 3}} = 2 \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(1) + f'(1)(x − 1) \)
\( = 3 + 2(x - 1) \)
\( = 2x + 1 \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = 1 \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(1,245) = 2(1,245) + 1 = 3,49 \)
Fonksiyonun \( x = 1,245 \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz
\( f(1,245) = 3,5085\ldots \)
\( L(1,245) \approx f(1,245) \)
\( (0,95)^{1,95} \) ifadesinin yaklaşık değerini hesaplayın.
Çözümü Gösterİfadenin yaklaşık değerini bulmak için \( x^{x + 1} \) fonksiyonuna lineerleştirme yöntemini uygulayalım.
\( f(x) = x^{x + 1} \)
\( x = 0,95 \) noktasına en yakın ve fonksiyon değerini kolaylıkla hesaplayabileceğimiz değer \( x = 1 \) değeridir.
Fonksiyona \( a = 1 \) apsisli noktada teğet olan doğrunun denklemini bulalım.
\( L(x) = f(a) + f'(a)(x - a) \)
\( = f(1) + f'(1)(x − 1) \)
\( f(1) = 1^{1 + 1} = 1 \)
\( f \) fonksiyonunun türevini logaritma ile türev alma yöntemi ile aşağıdaki şekilde bulabiliriz.
\( f'(x) = x^{x + 1}(\ln{x} + \dfrac{x + 1}{x}) \)
\( f'(1) = 1^{1 + 1}(\ln{1} + \dfrac{1 + 1}{1}) \)
\( = 1(0 + 2) = 2 \)
Bulduğumuz değerleri teğet doğru denkleminde yerine koyalım.
\( L(x) = f(1) + f'(1)(x − 1) \)
\( = 1 + 2(x − 1) = 2x - 1 \)
Buna göre bulduğumuz \( L(x) \) doğrusunun \( x = 1 \) noktasına yakın noktalarda \( f \) fonksiyonu ile yakın değerlere sahip olacağını söyleyebiliriz.
\( L(0,95) = 2(0,95) - 1 = 0,90 \)
Fonksiyonun \( x = 0,95 \) noktasındaki gerçek değerini hesap makinesi ile hesapladığımızda, bulduğumuz yaklaşık değerin gerçek değere oldukça yakın olduğunu görebiliriz.
\( f(0,95) = (0,95)^{1,95} = 0,9048\ldots \)
\( L(0,95) \approx f(0,95) \)