Artan ve Azalan Aralıkların Bulunması
Konu tekrarı için: Artan ve Azalan Fonksiyonlar
Bir fonksiyonun birinci türevi bir noktadaki anlık değişim oranını verdiği için, birinci türevin (teğet doğrunun eğiminin) belirli bir aralıktaki işareti fonksiyonun bu aralıkta artan, azalan ya da sabit olması hakkında bilgi verir.
Aşağıdaki grafikte bir fonksiyonun artan ve azalan olduğu aralıklar ve birinci türevi arasındaki ilişki gösterilmiştir. Şekilde ana fonksiyonun grafiği üzerindeki \( + \) ve \( - \) işaretleri fonksiyonun değerinin değil, eğiminin işaretini göstermektedir.
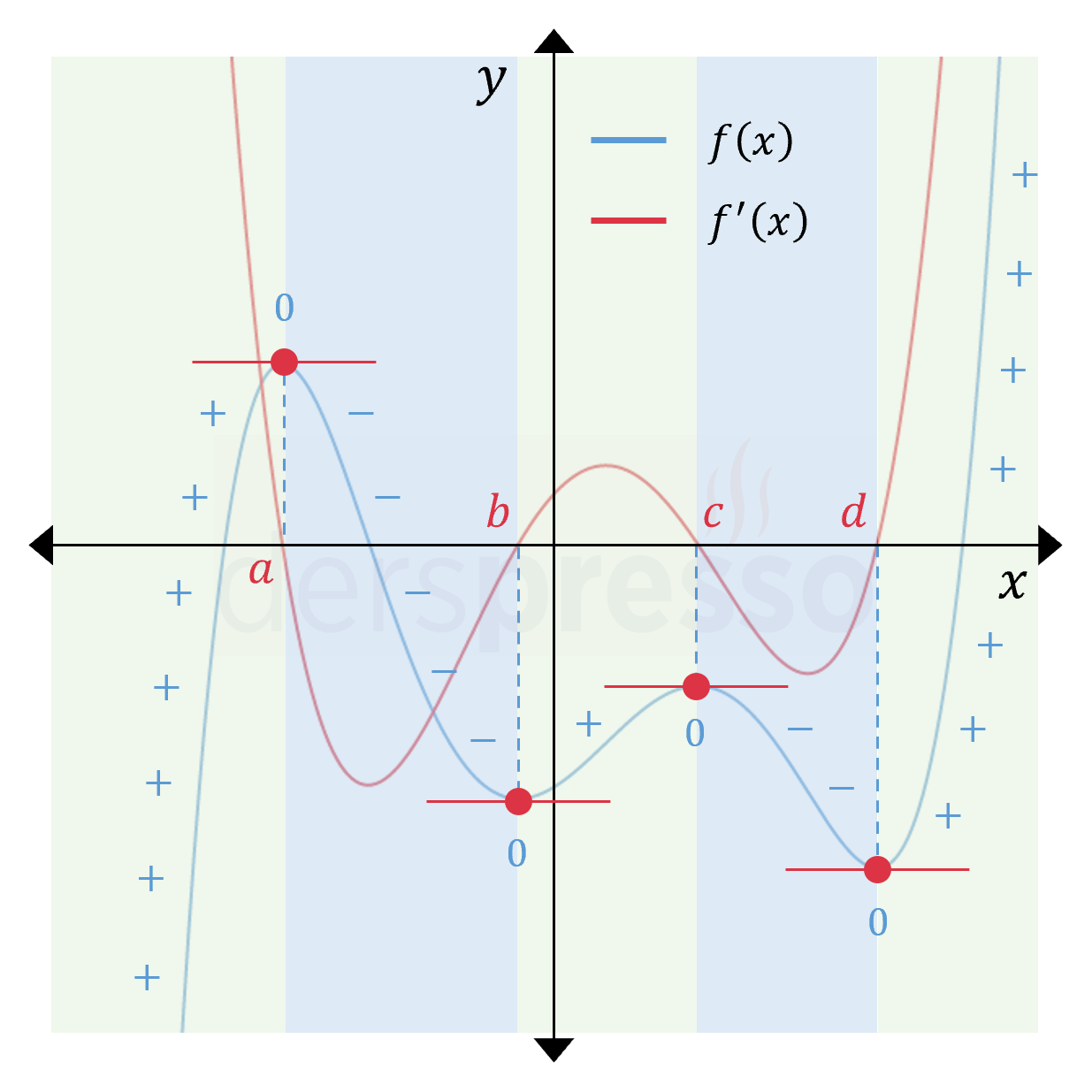
Buna göre ana fonksiyonun artan olduğu aralıklarda (yeşil zemin rengi) birinci türev pozitif, azalan olduğu aralıklarda (mavi zemin rengi) birinci türev negatif olur. Ana fonksiyonun durağan olduğu \( a \), \( b \), \( c \), \( d \) noktalarında ise birinci türev sıfır olur.
\( f \) fonksiyonu \( (a, b) \) aralığında türevlenebilir olmak üzere,
Her \( x \in (a, b) \) değeri için,
- \( f'(x) \gt 0 \) ise \( f \) fonksiyonu bu aralıkta artandır.
- \( f'(x) \lt 0 \) ise \( f \) fonksiyonu bu aralıkta azalandır.
- \( f'(x) = 0 \) ise \( f \) fonksiyonu bu aralıkta sabittir.
Dolayısıyla, bir fonksiyonun (yukarıdaki süreklilik ve türevlenebilirlik koşullarını sağladığı bir tanım aralığında) artan olduğu aralıkları bulmak için birinci türevin pozitif olduğu, azalan olduğu aralıkları bulmak için de birinci türevin negatif olduğu aralıklar bulunur.
Bir \( f \) fonksiyonunun;
- Artan olduğu aralıkları bulmak için \( f'(x) \gt 0 \) eşitsizliği çözülür.
- Azalan olduğu aralıkları bulmak için \( f'(x) \lt 0 \) eşitsizliği çözülür.
\( f(x) = x^4 - 2x^3 - 20x^2 + 5 \) fonksiyonunun artan ve azalan olduğu aralıkları bulalım.
Bir fonksiyon birinci türevinin pozitif olduğu aralıklarda artan, negatif olduğu aralıklarda azalandır.
Fonksiyonun birinci türevini bulalım.
\( f'(x) = 4x^3 - 6x^2 - 40x \)
Polinom ifadesini çarpanlarına ayıralım.
\( = 2x(2x + 5)(x - 4) \)
Her bir çarpanı sıfır yapan \( x \in \{ 0, -\frac{5}{2}, 4 \} \) noktalarında birinci türev sıfır olur, dolayısıyla bu noktalar fonksiyonun durağan noktalarıdır.
Bu noktalar arasında kalan aralıklarda birinci türevin işaretini bulmak için bir işaret tablosu hazırlayalım.
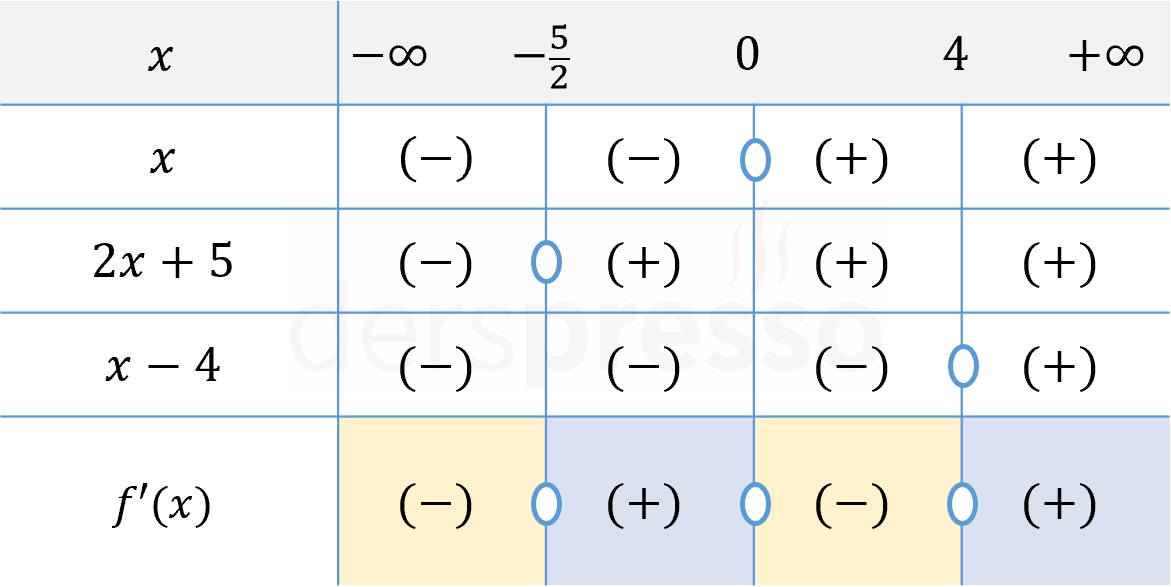
Buna göre fonksiyonun \( (-\infty, -\frac{5}{2}) \) ve \( (0, 4) \) aralıklarında birinci türevi negatiftir, dolayısıyla fonksiyon bu iki aralıkta azalandır.
Fonksiyonun \( (-\frac{5}{2}, 0) \) ve \( (4, \infty) \) aralıklarında ise birinci türevi pozitiftir, dolayısıyla fonksiyon bu iki aralıkta artandır.
Aşağıdaki fonksiyonların artan olduğu aralıkları bulunuz.
(a) \( f(x) = \dfrac{1}{3}x^3 - 2x^2 + 3x + 6 \)
(b) \( g(x) = 2x^3 - 6x + 4 \)
(c) \( h(x) = -x^3 - \dfrac{9}{2}x^2 + 30x - 8 \)
Çözümü GösterBir fonksiyon birinci türevinin (eğiminin) pozitif olduğu aralıklarda artan, negatif olduğu aralıklarda azalandır.
(a) seçeneği:
\( f(x) = \dfrac{1}{3}x^3 - 2x^2 + 3x + 6 \)
Fonksiyonun birinci türevini alalım.
\( f'(x) = x^2 - 4x + 3 \)
Birinci türevin pozitif olduğu aralıkları bulalım.
\( f'(x) = x^2 - 4x + 3 \gt 0 \)
\( (x - 1)(x - 3) \gt 0 \)
Bu eşitsizlik aşağıdaki aralıkta sağlandığı için fonksiyon bu aralıkta artandır.
\( x \in (-\infty, 1) \cup (3, \infty) \)
(b) seçeneği:
\( g(x) = 2x^3 - 6x + 4 \)
Fonksiyonun birinci türevini alalım.
\( g'(x) = 6x^2 - 6 \)
Birinci türevin pozitif olduğu aralıkları bulalım.
\( g'(x) = 6x^2 - 6 \gt 0 \)
\( 6(x - 1)(x + 1) \gt 0 \)
Bu eşitsizlik aşağıdaki aralıkta sağlandığı için fonksiyon bu aralıkta artandır.
\( x \in (-\infty, -1) \cup (1, \infty) \)
(c) seçeneği:
\( h(x) = -x^3 - \dfrac{9}{2}x^2 + 30x - 8 \)
Fonksiyonun birinci türevini alalım.
\( h'(x) = -3x^2 - 9x + 30 \)
Birinci türevin pozitif olduğu aralıkları bulalım.
\( h'(x) = -3x^2 - 9x + 30 \gt 0 \)
\( -3(x + 5)(x - 2) \gt 0 \)
Bu eşitsizlik aşağıdaki aralıkta sağlandığı için fonksiyon bu aralıkta artandır.
\( x \in (-5, 2) \)
Aşağıdaki fonksiyonların azalan olduğu aralıkları bulunuz.
(a) \( f(x) = 2x^3 - 4x^2 + 10 \)
(b) \( g(x) = 2 - 5x^2 - 10x^3 \)
(c) \( h(x) = 4x^3 + 3x^2 - 6x \)
Çözümü GösterBir fonksiyon birinci türevinin (eğiminin) pozitif olduğu aralıklarda artan, negatif olduğu aralıklarda azalandır.
(a) seçeneği:
\( f(x) = 2x^3 - 4x^2 + 10 \)
Fonksiyonun birinci türevini alalım.
\( f'(x) = 6x^2 - 8x \)
Birinci türevin negatif olduğu aralıkları bulalım.
\( f'(x) = 6x^2 - 8x \lt 0 \)
\( 2x(3x - 4) \lt 0 \)
Bu eşitsizlik aşağıdaki aralıkta sağlandığı için fonksiyon bu aralıkta azalandır.
\( x \in (0, \frac{4}{3}) \)
(b) seçeneği:
\( g(x) = 2 - 5x^2 - 10x^3 \)
Fonksiyonun birinci türevini alalım.
\( g'(x) = -10x - 30x^2 \)
Birinci türevin negatif olduğu aralıkları bulalım.
\( g'(x) = -10x - 30x^2 \lt 0 \)
\( -10x(1 + 3x) \lt 0 \)
Bu eşitsizlik aşağıdaki aralıkta sağlandığı için fonksiyon bu aralıkta azalandır.
\( x \in (-\infty, -\frac{1}{3}) \cup (0, \infty) \)
(c) seçeneği:
\( h(x) = 4x^3 + 3x^2 - 6x \)
Fonksiyonun birinci türevini alalım.
\( h'(x) = 12x^2 + 6x - 6 \)
Birinci türevin negatif olduğu aralıkları bulalım.
\( h'(x) = 12x^2 + 6x - 6 \lt 0 \)
\( 6(2x - 1)(x + 1) \lt 0 \)
Bu eşitsizlik aşağıdaki aralıkta sağlandığı için fonksiyon bu aralıkta azalandır.
\( x \in (-1, \frac{1}{2}) \)
\( f: \mathbb{R} - \{a\} \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{x + 8}{x - a} \) fonksiyonu daima artan olduğuna göre, \( a \)'nın alabileceği en büyük tam sayı değeri kaçtır?
Çözümü GösterBir fonksiyon birinci türevinin (eğiminin) pozitif olduğu aralıkta artandır.
Buna göre fonksiyon daima artan ise tüm tanım aralığında \( f'(x) \gt 0 \) olmalıdır.
Fonksiyonun türevini almak için bölme kuralını uygulayalım.
\( f'(x) = \dfrac{(x + 8)'(x - a) - (x + 8)(x - a)'}{(x - a)^2} \)
\( = \dfrac{-a - 8}{(x - a)^2} \)
Paydadaki ifade fonksiyonun tanım kümesi içinde her zaman pozitiftir. Buna göre paydaki ifade pozitif olduğunda birinci türev pozitif olur.
\( f'(x) \gt 0 \)
\( -a - 8 \gt 0 \)
\( a \lt -8 \)
Buna göre \( a \)'nın alabileceği en büyük tam sayı değeri \( -9 \) olur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2e^x \) fonksiyonunun artan olduğu aralığı bulunuz.
Çözümü GösterBir fonksiyon birinci türevinin (eğiminin) pozitif olduğu aralıklarda artandır.
Fonksiyonun türevini alalım.
\( f'(x) = 2xe^x + x^2e^x \)
Birinci türevin pozitif olduğu aralığı bulalım.
\( 2xe^x + x^2e^x \gt 0 \)
\( xe^x(x + 2) \gt 0 \)
Birinci türev fonksiyonu için bir işaret tablosu oluşturalım.
\( e^x \) ifadesi tüm reel sayılarda pozitiftir.
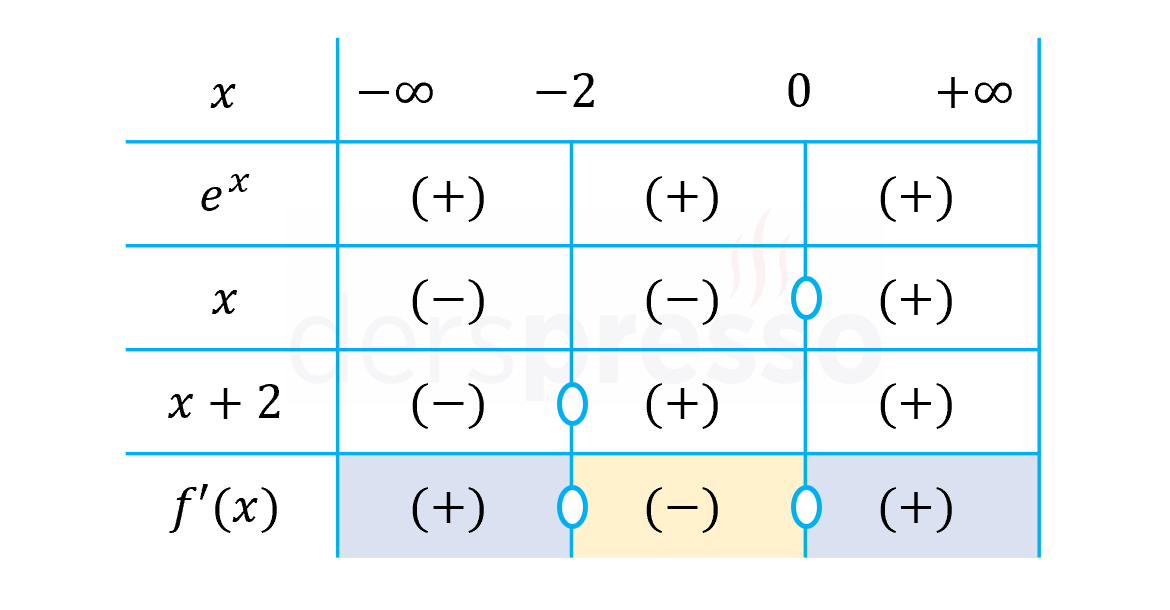
Buna göre, \( f' \) fonksiyonu \( (-\infty, -2) \) ve \( (0, \infty) \) aralıklarında pozitiftir, dolayısıyla \( f \) fonksiyonu bu iki aralıkta artandır.
\( f(x) = 2x^3 - 12x^2 - 30x + 11 \)
\( g(x) = 4x^2 - 24x + 17 \)
Yukarıdaki iki fonksiyondan birinin artarken diğerinin azaldığı aralıklar nedir?
Çözümü GösterBir fonksiyon birinci türevinin (eğiminin) pozitif olduğu aralıklarda artar, negatif olduğu aralıklarda azalır.
Fonksiyonların birinci türevini alalım.
\( f'(x) = 6x^2 - 24x - 30 \)
\( = 6(x + 1)(x - 5) \)
\( f' \) fonksiyonu \( x = -1 \) ve \( x = 5 \) noktaları arasında kalan \( (-1, 5) \) aralığında negatiftir, dışında kalan aralıkta pozitiftir. Dolayısıyla \( f \) fonksiyonu bu iki aralıkta sırasıyla azalan ve artandır.
\( g'(x) = 8x - 24 \)
\( = 8(x - 3) \)
\( g' \) fonksiyonu \( x = 3 \) noktasının solunda kalan \( (-\infty, 3) \) aralığında negatiftir, sağında kalan \( (3, \infty) \) aralığında pozitiftir. Dolayısıyla \( g \) fonksiyonu bu iki aralıkta sırasıyla azalan ve artandır.
İki fonksiyonun türevinin farklı aralıklardaki işaretleri için bir işaret tablosu hazırlayalım.
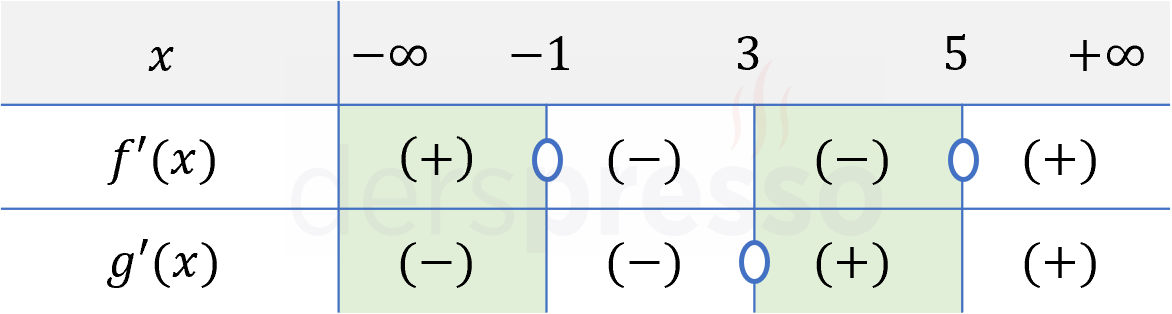
Buna göre \( (-\infty, -1) \) aralığında \( f \) fonksiyonu artarken \( g \) fonksiyonu azalır. \( (3, 5) \) aralığında ise \( f \) fonksiyonu azalırken \( g \) fonksiyonu artar.
\( x^9 + x^7 + x^5 + 1 = 0 \) denkleminin kaç reel kökü vardır?
Çözümü GösterEşitliğin sol tarafındaki ifadeyi bir polinom fonksiyonu şeklinde tanımlayalım.
\( f(x) = x^9 + x^7 + x^5 + 1 \)
Buna göre \( f \) fonksiyonunun grafiğinin \( x \) eksenini kaç noktada kestiği sorulmaktadır.
Fonksiyonun türevini alalım.
\( f'(x) = 9x^8 + 7x^6 + 5x^4 \)
Türev fonksiyonundaki terimlerin tümü çift dereceli olduğu için türev hiçbir zaman negatif değer almaz, dolayısıyla \( f \) fonksiyonu tüm reel sayılarda artandır.
Tek dereceli polinom fonksiyonlarının en az bir reel kökü vardır. Tüm reel sayılarda artan olan fonksiyon bu kök değerinden sonra ikinci bir kök için azalan olamayacağı için fonksiyonun tek bir reel sayı kökü vardır.
\( P(x) \) polinom fonksiyonu tüm reel sayılarda azalandır.
\( a \lt b \) olduğuna göre, aşağıdaki ifadelerden hangileri kesinlikle doğrudur?
I. \( P(a) \ge P(b) \)
II. \( P'(a) \ge P'(b) \)
III. \( P''(a) \ge P''(b) \)
Çözümü GösterBir fonksiyonun bir aralıkta azalan olabilmesi için fonksiyon değeri o aralıkta azalabilir ya da sabit kalabilir, ama artamaz.
Fonksiyon azalan ise \( P(b) \) değeri \( P(a) \) değerine eşit ya da ondan küçük olmalıdır. Buna göre I. öncül her zaman doğrudur.
Bir fonksiyonun azalan olduğu aralıkta birinci türevi sıfır ya da negatif olur, dolayısıyla \( P'(a) \le 0 \) ve \( P'(b) \le 0 \) olduğunu söyleyebiliriz, ancak bu iki noktadaki birinci türev değerleri arasında bir karşılaştırma yapamayız.
Bir fonksiyon azalan olduğu bir aralıkta eğimi artıyor (\( P''(x) \gt 0 \)), azalıyor (\( P''(x) \lt 0 \)) ya da sabit kalıyor (\( P''(x) = 0 \)) olabilir. Bu yüzden bu iki noktadaki ikinci türev değerleri arasında bir karşılaştırma yapamayız.
Sadece I. öncül kesinlikle doğrudur.
\( f(x) = \sin{x} + kx \) fonksiyonunun ters fonksiyonunun tanımlı olabilmesi için \( k \) değer aralığı ne olmalıdır?
Çözümü GösterBir fonksiyonunun ters fonksiyonunun tanımlı olması için fonksiyon birebir olmalıdır.
Bir fonksiyonun birebir olması için grafiği kesin artan ya da kesin azalan olmalıdır, aksi takdirde fonksiyon belirli bir \( y \) değerini birden fazla \( x \) değerinde alır.
Verilen fonksiyonun türevini alalım.
\( f'(x) = \cos{x} + k \)
Fonksiyonun kesin artan olması için birinci türevi tüm reel sayılarda pozitif, kesin azalan olması için tüm reel sayılarda negatif olmalıdır.
Durum 1: Kesin artan
\( f'(x) = \cos{x} + k \gt 0 \)
Kosinüs fonksiyonu \( [-1, 1] \) aralığında değer alır.
Bu eşitsizliğin her \( x \) değeri için sağlanması için \( k \gt 1 \) olmalıdır.
Durum 2: Kesin azalan
\( f'(x) = \cos{x} + k \lt 0 \)
Bu eşitsizliğin her \( x \) değeri için sağlanması için \( k \lt -1 \) olmalıdır.
Bu iki durumdan birinin sağlandığı durumda fonksiyon birebir olacağı için \( k \) değer aralığı bulduğumuz iki aralığın birleşim kümesi olur.
\( k \in (-\infty, -1) \cup (1, \infty) \)